题目内容
 如图,在Rt△ABC中,∠ACB=90°,以AC为一边向外作等边三角形ACD,点E为AB的中点,连接CE、DE.
如图,在Rt△ABC中,∠ACB=90°,以AC为一边向外作等边三角形ACD,点E为AB的中点,连接CE、DE.(1)若∠BAC=40°,求∠DEC的度数;
(2)当四边形DCBE是平行四边形时,求∠BAC的度数;
(3)若△ADE的面积是△CBE的面积的
| 4 |
| 3 |
考点:全等三角形的判定与性质,等边三角形的性质,平行四边形的性质,解直角三角形
专题:
分析:(1)可以判定DE是AC的垂直平分线,根据平行线性质即可求得∠DEC度数;
(2)根据BC=2OE,可以求得AD=AE,可以证明RT△ADO≌RT△AEO,即可得∠BAC=∠DAC;
(3)根据△ADE的面积和△CBE的面积比可以求得OD和BC的长度关系比,即可求得AC和BC长度关系比,根据∠ACE=∠BAC即可解题.
(2)根据BC=2OE,可以求得AD=AE,可以证明RT△ADO≌RT△AEO,即可得∠BAC=∠DAC;
(3)根据△ADE的面积和△CBE的面积比可以求得OD和BC的长度关系比,即可求得AC和BC长度关系比,根据∠ACE=∠BAC即可解题.
解答:解:(1)∵E是AB中点,
∴AE=EC,
∵AD=CD,
∴DE是AC垂直平分线,
∴AC⊥DE,
∴DE∥BC,
∴∠BAC=∠ACE=40°,
∴∠DEC=∠BCE=50°;
(2)如图,
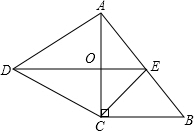
∵四边形DCBE是平行四边形,
∴DE=BC,
∵OE=
BC,
∴OD=
BC=OE,
∵AD=
,AE=
,
∴AD=AE,
∵在RT△ADO和RT△AEO中,
,
∴RT△ADO≌RT△AEO,(HL)
∴∠BAC=∠DAC=60°;
(3)∵△ADE的面积是△CBE的面积的
倍,∴DE=
BC,
∵OE=
BC,
∴OD=
BC,
∴AC=
×
BC,
∴tan∠BAC=
=
.
∴tan∠ACE=
.
∴AE=EC,
∵AD=CD,
∴DE是AC垂直平分线,
∴AC⊥DE,
∴DE∥BC,
∴∠BAC=∠ACE=40°,
∴∠DEC=∠BCE=50°;
(2)如图,

∵四边形DCBE是平行四边形,
∴DE=BC,
∵OE=
| 1 |
| 2 |
∴OD=
| 1 |
| 2 |
∵AD=
| OD2+OA2 |
| AO2+EO2 |
∴AD=AE,
∵在RT△ADO和RT△AEO中,
|
∴RT△ADO≌RT△AEO,(HL)
∴∠BAC=∠DAC=60°;
(3)∵△ADE的面积是△CBE的面积的
| 4 |
| 3 |
| 4 |
| 3 |
∵OE=
| 1 |
| 2 |
∴OD=
| 5 |
| 6 |
∴AC=
| 5 |
| 6 |
| 2 | ||
|
∴tan∠BAC=
| BC |
| AC |
3
| ||
| 5 |
∴tan∠ACE=
3
| ||
| 5 |
点评:本题考查了全等三角形判定,考查了全等三角形对应角相等的性质,本题中求证RT△ADO≌RT△AEO是解题的关键.

练习册系列答案
相关题目
甲乙两地相距20千米,某人从甲地去乙地,先步行走了8千米,又骑自行车到达乙地,共用了3小时,如果这个人骑自行车的速度是步行速度的3倍,那么他步行的速度是( )
| A、4千米/时 |
| B、6千米/时 |
| C、3千米/时 |
| D、8千米/时 |
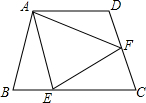 如图,在四边形ABCD中,AB=AD,∠ABC+∠ADC=180°.E,F分别是BC,CD上的点,且∠EAF=
如图,在四边形ABCD中,AB=AD,∠ABC+∠ADC=180°.E,F分别是BC,CD上的点,且∠EAF=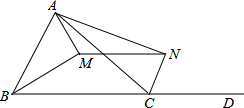 如图,BM平分∠ABC,AM⊥BM,CN平分∠ACD,AN⊥CN.请问:MN与AB、BC、AC之间的关系,并证明.
如图,BM平分∠ABC,AM⊥BM,CN平分∠ACD,AN⊥CN.请问:MN与AB、BC、AC之间的关系,并证明.