题目内容
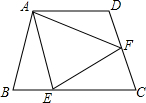 如图,在四边形ABCD中,AB=AD,∠ABC+∠ADC=180°.E,F分别是BC,CD上的点,且∠EAF=
如图,在四边形ABCD中,AB=AD,∠ABC+∠ADC=180°.E,F分别是BC,CD上的点,且∠EAF=| 1 |
| 2 |
考点:旋转的性质,全等三角形的判定与性质
专题:常规题型
分析:把△ADF绕点A顺时针旋转∠DAB的度数得到△ABG,如图,根据旋转的性质得到∠ADF=∠ABG,∠GAF=∠BAD,AG=AF,BG=DF,再证明点G在CB的延长线上,
即GE=BG+BE,然后证明△AEG≌△AEF,得到EF=GE,所以EF=BE+BG=BE+DF.
即GE=BG+BE,然后证明△AEG≌△AEF,得到EF=GE,所以EF=BE+BG=BE+DF.
解答: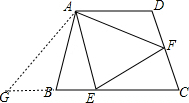 解:EF=BE+DF.理由如下:
解:EF=BE+DF.理由如下:
把△ADF绕点A顺时针旋转∠DAB的度数得到△ABG,如图,
∴∠ADF=∠ABG,∠GAF=∠BAD,AG=AF,BG=DF,
∵∠ABC+∠ADC=180°,
∴∠ABC+∠ABG=180°,
∴点G在CB的延长线上,
∴GE=BG+BE,
∵∠EAF=
∠BAD,
∴∠EAF=
∠GAE,
∴∠EAF=∠GAE,
在△AEG和△AEF中,
,
∴△AEG≌△AEF(SAS),
∴EF=GE,
∴EF=BE+BG=BE+DF.
 解:EF=BE+DF.理由如下:
解:EF=BE+DF.理由如下:把△ADF绕点A顺时针旋转∠DAB的度数得到△ABG,如图,
∴∠ADF=∠ABG,∠GAF=∠BAD,AG=AF,BG=DF,
∵∠ABC+∠ADC=180°,
∴∠ABC+∠ABG=180°,
∴点G在CB的延长线上,
∴GE=BG+BE,
∵∠EAF=
| 1 |
| 2 |
∴∠EAF=
| 1 |
| 2 |
∴∠EAF=∠GAE,
在△AEG和△AEF中,
|
∴△AEG≌△AEF(SAS),
∴EF=GE,
∴EF=BE+BG=BE+DF.
点评:本题考查了旋转的性质:对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角;旋转前、后的图形全等.也考查了全等三角形的判定与性质.

练习册系列答案
相关题目
 如图,△ABC中,DE∥BC,DF∥AC,求证:△ADE∽△DBF.
如图,△ABC中,DE∥BC,DF∥AC,求证:△ADE∽△DBF. 如图,∠ABE=∠AFE=90°,AB=3,BE=
如图,∠ABE=∠AFE=90°,AB=3,BE= 如图,在Rt△ABC中,∠ACB=90°,以AC为一边向外作等边三角形ACD,点E为AB的中点,连接CE、DE.
如图,在Rt△ABC中,∠ACB=90°,以AC为一边向外作等边三角形ACD,点E为AB的中点,连接CE、DE.