题目内容
小明用12元买软面笔记本,小丽用21元买硬面笔记本.
(1)已知每本硬面笔记本比软面笔记本贵1.2元,小明和小丽能买到相同数量的笔记本吗?
(2)已知每本硬面笔记本比软面笔记本贵a元,是否存在正整数a,使得每本硬面笔记本、软面笔记本的价格都是正整数,并且小明和小丽能买到相同数量的笔记本?若存在,求出a的值;若不存在,请说明理由.
(1)已知每本硬面笔记本比软面笔记本贵1.2元,小明和小丽能买到相同数量的笔记本吗?
(2)已知每本硬面笔记本比软面笔记本贵a元,是否存在正整数a,使得每本硬面笔记本、软面笔记本的价格都是正整数,并且小明和小丽能买到相同数量的笔记本?若存在,求出a的值;若不存在,请说明理由.
考点:分式方程的应用
专题:
分析:(1)设每本软面笔记本x元,则每本硬面笔记本(x+1.2)元,根据小明和小丽能买到相同数量的笔记本建立方程求出其解就可以得出结论;
(2)设每本软面笔记本m元(1≤m≤12的整数),则每本硬面笔记本(m+a)元,根据小明和小丽能买到相同数量的笔记本建立方程就可以得出m与a的关系,就可以求出结论.
(2)设每本软面笔记本m元(1≤m≤12的整数),则每本硬面笔记本(m+a)元,根据小明和小丽能买到相同数量的笔记本建立方程就可以得出m与a的关系,就可以求出结论.
解答:解:(1))设每本软面笔记本x元,则每本硬面笔记本(x+1.2)元,由题意,得
=
,
解得:x=1.6.
此时
=
=7.5(不符合题意),
所以,小明和小丽不能买到相同数量的笔记本;
(2)设每本软面笔记本m元(1≤m≤12的整数),则每本硬面笔记本(m+a)元,由题意,得
=
,
解得:a=
m,
∵a为正整数,
∴m=4,8,12.
∴a=3,6,9.
当
时,
=
=1.5(不符合题意)
∴a的值为3或9.
| 12 |
| x |
| 21 |
| x+1.2 |
解得:x=1.6.
此时
| 12 |
| 1.6 |
| 21 |
| 1.2+1.6 |
所以,小明和小丽不能买到相同数量的笔记本;
(2)设每本软面笔记本m元(1≤m≤12的整数),则每本硬面笔记本(m+a)元,由题意,得
| 12 |
| m |
| 21 |
| m+a |
解得:a=
| 3 |
| 4 |
∵a为正整数,
∴m=4,8,12.
∴a=3,6,9.
当
|
| 12 |
| m |
| 21 |
| m+a |
∴a的值为3或9.
点评:本题考查了列分式方程解实际问题的运用,分式方程的解法的运用,二元一次不定方程的解法的运用,解答时求出根据两种笔记本购买的数量相等建立方程是关键.

练习册系列答案
相关题目
下列说法中,错误的是( )
| A、除三角形外的多边形都有对角线 |
| B、任意四边形的内角和等于外角和 |
| C、过n边形的一个顶点有(n-3)条对角线 |
| D、(n+1)边形的内角和比n边形的内角和大360° |
a是最小的正整数,b是最大的负整数,c是绝对值最小的有理数,则a+b+c为( )
| A、-1 | B、0 | C、1 | D、2 |
 如图,E是△ABC边AC上一点,O为BE的中点,过点B作AC的平行线与AO的延长线相交于点D,连接DE,那么DE与AB有怎样的数量和位置关系?
如图,E是△ABC边AC上一点,O为BE的中点,过点B作AC的平行线与AO的延长线相交于点D,连接DE,那么DE与AB有怎样的数量和位置关系?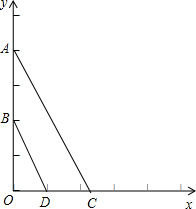 已知:如图,在平面直角坐标系xOy中,A(0,4),B(0,2),点C在x轴的正半轴上,点D为OC的中点.
已知:如图,在平面直角坐标系xOy中,A(0,4),B(0,2),点C在x轴的正半轴上,点D为OC的中点.