题目内容
20.已知a、b、c是三角形的三边长,如果满足(a-6)2+|b-8|+$\sqrt{c-10}$=0,则三角形的形状是( )| A. | 底与边不相等的等腰三角形 | B. | 等边三角形 | ||
| C. | 钝角三角形 | D. | 直角三角形 |
分析 根据非负数的性质可得a-6=0,b-8=0,c-10=0,再解方程可得a、b、c的值,再利用勾股定理逆定理可得三角形的形状.
解答 解:由题意得:a-6=0,b-8=0,c-10=0,
解得:a=6,b=8,c=10,
∵62+82=102,
∴三角形为直角三角形,
故选D
点评 此题主要考查了非负数的性质,以及勾股定理逆定理,关键是掌握勾股定理的逆定理:如果三角形的三边长a,b,c满足a2+b2=c2,那么这个三角形就是直角三角形.

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案
相关题目
8.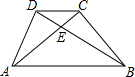 如图,梯形ABCD中,AB∥CD,AC、BD交于E,若S△DCE:S△BAE=1:9,则S△DCE:S△BCE为( )
如图,梯形ABCD中,AB∥CD,AC、BD交于E,若S△DCE:S△BAE=1:9,则S△DCE:S△BCE为( )
 如图,梯形ABCD中,AB∥CD,AC、BD交于E,若S△DCE:S△BAE=1:9,则S△DCE:S△BCE为( )
如图,梯形ABCD中,AB∥CD,AC、BD交于E,若S△DCE:S△BAE=1:9,则S△DCE:S△BCE为( )| A. | 1:9 | B. | 1:4 | C. | 1:3 | D. | 9:1 |
10.-|-$\frac{3}{5}$|的负倒数是( )
| A. | $-\frac{5}{3}$ | B. | $\frac{5}{3}$ | C. | $-\frac{3}{5}$ | D. | $\frac{3}{5}$ |
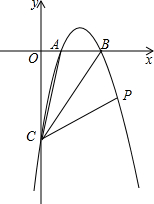 如图,抛物线y=-x2+3x-2与x轴交于A、B两点,与y轴交于C点,点P在抛物线上,∠ACB=∠BCP,求P点的坐标.
如图,抛物线y=-x2+3x-2与x轴交于A、B两点,与y轴交于C点,点P在抛物线上,∠ACB=∠BCP,求P点的坐标.