题目内容
2. 如图,将Rt△ABC绕直角顶点C顺时针旋转90°,得到△A′B′C,连接AA′,若∠1=25°,则∠BAA′的度数是( )
如图,将Rt△ABC绕直角顶点C顺时针旋转90°,得到△A′B′C,连接AA′,若∠1=25°,则∠BAA′的度数是( )| A. | 55° | B. | 60° | C. | 65° | D. | 70° |
分析 根据旋转的性质可得AC=A′C,然后判断出△ACA′是等腰直角三角形,根据等腰直角三角形的性质可得∠CAA′=45°,再根据三角形的内角和定理可得结果.
解答 解:∵Rt△ABC绕直角顶点C顺时针旋转90°得到△A′B′C,
∴AC=A′C,
∴△ACA′是等腰直角三角形,
∴∠CA′A=45°,∠CA′B′=20°=∠BAC
∴∠BAA′=180°-70°-45°=65°,
故选:C.
点评 本题考查了旋转的性质,等腰直角三角形的判定与性质,三角形的一个外角等于与它不相邻的两个内角的和的性质,熟记各性质并准确识图是解题的关键.

练习册系列答案
 全优点练单元计划系列答案
全优点练单元计划系列答案
相关题目
12.下列曲线中不能表示y是x的函数的是( )
| A. |  | B. |  | C. |  | D. |  |
11.下面四个数中比-5小的数是( )
| A. | 1 | B. | 0 | C. | -4 | D. | -6 |
12.某服装店用10000元购进一批某品牌夏季衬衫若干件,很快售完;该店又用14700元钱购进第二批这种衬衫,所进件数比第一批多40%,每件衬衫的进价比第一批每件衬衫的进价多10元,求第一批购进多少件衬衫?设第一批购进x件衬衫,则所列方程为( )
| A. | $\frac{10000}{x}$-10=$\frac{14700}{(1+40%)x}$ | B. | $\frac{10000}{x}$+10=$\frac{14700}{(1+40%)x}$ | ||
| C. | $\frac{10000}{(1-40%)x}$-10=$\frac{14700}{x}$ | D. | $\frac{10000}{(1-40%)x}$+10=$\frac{14700}{x}$ |
 如图,BC是⊙O的直径,点A在圆上,连接AO,AC,∠AOB=64°,则∠ACB=32°.
如图,BC是⊙O的直径,点A在圆上,连接AO,AC,∠AOB=64°,则∠ACB=32°.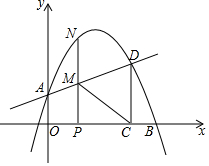 如图,在平面直角坐标系中,抛物线y=ax2+bx+1交y轴于点A,交x轴正半轴于点B(4,0),与过A点的直线相交于另一点D(3,$\frac{5}{2}$),过点D作DC⊥x轴,垂足为C.
如图,在平面直角坐标系中,抛物线y=ax2+bx+1交y轴于点A,交x轴正半轴于点B(4,0),与过A点的直线相交于另一点D(3,$\frac{5}{2}$),过点D作DC⊥x轴,垂足为C.