题目内容
10.在△ABC中,∠A:∠B:∠C=2:3:4,则∠A的度数为40°.分析 直接用一个未知数表示出∠A,∠B,∠C的度数,再利用三角形内角和定理得出答案.
解答 解:∵∠A:∠B:∠C=2:3:4,
∴设∠A=2x,∠B=3x,∠C=4x,
∵∠A+∠B+∠C=180°,
∴2x+3x+4x=180°,
解得:x=20°,
∴∠A的度数为:40°.
故答案为:40°.
点评 此题主要考查了三角形内角和定理,正确表示出各角度数是解题关键.

练习册系列答案
相关题目
1.计算x6÷x2正确的是( )
| A. | 3 | B. | x3 | C. | x4 | D. | x8 |
5.下列图标中,既是轴对称图形,又是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
2. 如图,将Rt△ABC绕直角顶点C顺时针旋转90°,得到△A′B′C,连接AA′,若∠1=25°,则∠BAA′的度数是( )
如图,将Rt△ABC绕直角顶点C顺时针旋转90°,得到△A′B′C,连接AA′,若∠1=25°,则∠BAA′的度数是( )
 如图,将Rt△ABC绕直角顶点C顺时针旋转90°,得到△A′B′C,连接AA′,若∠1=25°,则∠BAA′的度数是( )
如图,将Rt△ABC绕直角顶点C顺时针旋转90°,得到△A′B′C,连接AA′,若∠1=25°,则∠BAA′的度数是( )| A. | 55° | B. | 60° | C. | 65° | D. | 70° |
19.当k<0时,一次函数y=kx-k的图象不经过( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
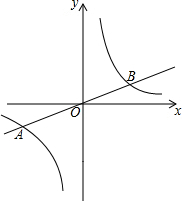 如图,在平面直角坐标系xOy中,已知正比例函数y=$\frac{1}{2}$x的图象与反比例函数y=$\frac{k}{x}$的图象交于A(a,-2),B两点.
如图,在平面直角坐标系xOy中,已知正比例函数y=$\frac{1}{2}$x的图象与反比例函数y=$\frac{k}{x}$的图象交于A(a,-2),B两点. 如图,直线EF∥GH,点A在EF上,AC交GH于点B,若∠FAC=72°,∠ACD=58°,点D在GH上,求∠BDC的度数.
如图,直线EF∥GH,点A在EF上,AC交GH于点B,若∠FAC=72°,∠ACD=58°,点D在GH上,求∠BDC的度数.