题目内容
 已知:如图,四边形ABCD内接于圆,DP∥CA交BA延长线于P.求证:AD•DC=PA•CB.
已知:如图,四边形ABCD内接于圆,DP∥CA交BA延长线于P.求证:AD•DC=PA•CB.考点:相似三角形的判定与性质,圆周角定理
专题:
分析:如图,作辅助线;证明∠PDA=∠DAC;证明∠PAD=∠DCB,得到△PDA∽△DBC,列出比例式即可解决问题.
解答: 证明:如图,连接BD;
证明:如图,连接BD;
则∠DBC=∠DAC;而DP∥CA,
∴∠PDA=∠DAC,
∴∠PDA=∠DBC,而∠PAD=∠DCB,
∴△PDA∽△DBC,
∴PA:DC=AD:BC,
即AD•DC=PA•CB.
 证明:如图,连接BD;
证明:如图,连接BD;则∠DBC=∠DAC;而DP∥CA,
∴∠PDA=∠DAC,
∴∠PDA=∠DBC,而∠PAD=∠DCB,
∴△PDA∽△DBC,
∴PA:DC=AD:BC,
即AD•DC=PA•CB.
点评:该题以圆为载体,主要考查了全等三角形的判定及其性质、圆周角定理及其推论等几何知识点的应用问题;解题的关键是作辅助线,准确找出命题图形中隐含的等量关系.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
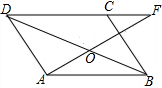 已知,如图,平行四边形ABCD中,F点是DC延长线上的一点,AF交BD于O,交BC于E.求证:
已知,如图,平行四边形ABCD中,F点是DC延长线上的一点,AF交BD于O,交BC于E.求证: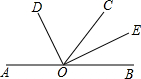 如图,O是直线AB上一点,OC为任一条射线,OD平分∠AOC,OE平分∠BOC.
如图,O是直线AB上一点,OC为任一条射线,OD平分∠AOC,OE平分∠BOC. 一个长方体的左视图,俯视图及相关数据如图所示,求其主视图的面积.
一个长方体的左视图,俯视图及相关数据如图所示,求其主视图的面积.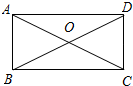 如图所示,在矩形ABCD中,对角线AC,BD相交于点O,∠AOD=120°,AB+AC=9,求对角线BD的长及矩形ABCD的面积.
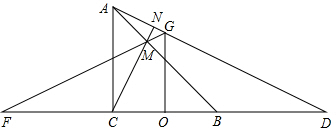
如图所示,在矩形ABCD中,对角线AC,BD相交于点O,∠AOD=120°,AB+AC=9,求对角线BD的长及矩形ABCD的面积. 如图,△ABC中,AB=BC,BE⊥AC于点E,AD⊥BC于点D,∠BAD=45°,AD与BE交于点F,连接CF.
如图,△ABC中,AB=BC,BE⊥AC于点E,AD⊥BC于点D,∠BAD=45°,AD与BE交于点F,连接CF.