Question

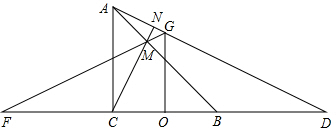
已知：如图∠ACB=90°，AC=BC．OG垂直平分BC，AG交CB的延长线于D，CN⊥AD于N，交AB于M，GM交BC的延长线于点F．求证：CF=BD．

Answer 1

考点：全等三角形的判定与性质

专题：证明题

分析：设OG、AB相交于E点，连结CE并延长交AD于H，如图，先根据等腰直角三角形的性质得∠2=45°，再利用OG垂直平分BC得到EB=EC，OB=OC，则∠3=∠2=45°，所以∠ACH=45°，接着利用等角的余角相等得到∠CAN=∠BCM，于是可利用“ASA”证明△ACH≌△CBM，得到CH=BM，所以EH=EM，然后再证明△GEH≌△GEM，得到∠EGH=∠EGM，即OG平分∠DGF，根据根据等腰三角形的性质得到OD=OF，则利用OB=OC，即可得到CF=BD．

解答：证明：设OG、AB相交于E点，连结CE并延长交AD于H，如图，
∵∠ACB=90°，AC=BC，
∴∠2=45°，
∵OG垂直平分BC，
∴EB=EC，OB=OC，
∴∠3=∠2=45°，
∴∠ACH=45°，
∵CN⊥AD，
∴∠1+∠CAN=45°，
而∠1+∠BCM=90°，
∴∠CAN=∠BCM，
在△ACH和△CBM中，

∠ACH=∠2 AC=CB ∠CAH=∠BCM

，
∴△ACH≌△CBM（ASA），
∴CH=BM，
∴EH=EM，
∵∠BEO=∠CEO=45°，
∴∠GEH=∠GEM=45°，
在△GEH和△GEM中，

GE=GE ∠GEH=∠GEM EH=EM

，
∴△GEH≌△GEM（SAS），
∴∠EGH=∠EGM，
即OG平分∠DGF，
而GO⊥DF，
∴OD=OF，
而OB=OC，
∴CF=BD．

点评：本题考查了全等三角形的判定与性质：全等三角形的判定是结合全等三角形的性质证明线段和角相等的重要工具．在判定三角形全等时，关键是选择恰当的判定条件．也考查了等腰三角形的判定与性质．