题目内容
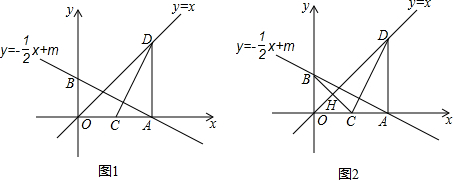
 如图,△ABC中,AB=BC,BE⊥AC于点E,AD⊥BC于点D,∠BAD=45°,AD与BE交于点F,连接CF.
如图,△ABC中,AB=BC,BE⊥AC于点E,AD⊥BC于点D,∠BAD=45°,AD与BE交于点F,连接CF.(1)求证:CD=DF;
(2)若CD=
| 2 |
考点:全等三角形的判定与性质,勾股定理
专题:
分析:(1)证明AD=BD,∠BFD=∠ACD,进而证明△BDF≌△ADC,即可解决问题.
(2)证明FA=FC;求出CF,即可解决问题.
(2)证明FA=FC;求出CF,即可解决问题.
解答: 解:(1)如图,∵AD⊥BC于点D,∠BAD=45°,
解:(1)如图,∵AD⊥BC于点D,∠BAD=45°,
∴∠ABD=90°-45°=45°,
∴∠ABD=∠BAD,AD=BD;
∵FD⊥DC,FE⊥CE,
∴∠FDC+∠FEC=180°,
∴E、F、D、C四点共圆,
∴∠BFD=∠ACD;
在△BDF与△ADC中,
,
∴△BDF≌△ADC(AAS),
∴CD=DF.
(2)∵AB=BC,BE⊥AC于点E,
∴AE=CE,即BE⊥AC且平分AC,
∴FA=FC;
∵FC2=2+2,
∴FA=FC=2,
∴BD=AD=2+
.
 解:(1)如图,∵AD⊥BC于点D,∠BAD=45°,
解:(1)如图,∵AD⊥BC于点D,∠BAD=45°,∴∠ABD=90°-45°=45°,
∴∠ABD=∠BAD,AD=BD;
∵FD⊥DC,FE⊥CE,
∴∠FDC+∠FEC=180°,
∴E、F、D、C四点共圆,
∴∠BFD=∠ACD;
在△BDF与△ADC中,
|
∴△BDF≌△ADC(AAS),
∴CD=DF.
(2)∵AB=BC,BE⊥AC于点E,
∴AE=CE,即BE⊥AC且平分AC,
∴FA=FC;
∵FC2=2+2,
∴FA=FC=2,
∴BD=AD=2+
| 2 |
点评:该题主要考查了全等三角形的判定、等腰直角三角形的性质、勾股定理等几何知识点的应用问题;应牢固掌握全等三角形的判定、等腰直角三角形的性质等几何知识点,灵活运用、解题.

练习册系列答案
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
如图,下列图中可以作为一个正方体的展开图的是( )
A、 |
B、 |
C、 |
D、 |
 如图,在长为32m,宽为20m的矩形耕地上,修筑同样宽的三条道路,使得剩余面积作为实验田,要使试验田面积为570m2,道路的宽应为多少?
如图,在长为32m,宽为20m的矩形耕地上,修筑同样宽的三条道路,使得剩余面积作为实验田,要使试验田面积为570m2,道路的宽应为多少? 已知:如图,四边形ABCD内接于圆,DP∥CA交BA延长线于P.求证:AD•DC=PA•CB.
已知:如图,四边形ABCD内接于圆,DP∥CA交BA延长线于P.求证:AD•DC=PA•CB.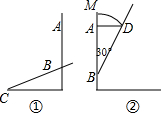 如图①,AB是房间的一面窗户的高,A是窗户上端,B是窗户下端,太阳光按BC的方向射入房间.
如图①,AB是房间的一面窗户的高,A是窗户上端,B是窗户下端,太阳光按BC的方向射入房间.