题目内容
 如图,PA、PB分别切⊙O于A、B两点,射线PD与⊙O相交于C,D两点,点E是CD中点,若∠APB=40°,则∠AEP的度数是( )
如图,PA、PB分别切⊙O于A、B两点,射线PD与⊙O相交于C,D两点,点E是CD中点,若∠APB=40°,则∠AEP的度数是( )| A、40° | B、50° |
| C、60° | D、70° |
考点:切线的性质
专题:
分析:连接OP,OA,OE,先根据垂径定理求得∠PEO=90°,然后根据切线的性质求得,∠APO=∠BPQ=
∠APB=20°∠PAO=90°,即可进一步证得A、O、E、P四点共圆,根据圆周角的性质即可求得.
| 1 |
| 2 |
解答: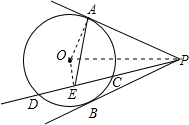 解:连接OP,OA,OE,
解:连接OP,OA,OE,
∵点E是CD中点,
∴OE⊥DC,
∴∠PEO=90°,
∵PA、PB分别切⊙O于A、B两点,
∴OA⊥PA,∠APO=∠BPQ=
∠APB=20°
∴∠PAO=90°,
∴∠POA=70°,
∴A、O、E、P四点在以OP为直径的圆上,
∴∠AEP=∠AOP=70°,
故选D.
 解:连接OP,OA,OE,
解:连接OP,OA,OE,∵点E是CD中点,
∴OE⊥DC,
∴∠PEO=90°,
∵PA、PB分别切⊙O于A、B两点,
∴OA⊥PA,∠APO=∠BPQ=
| 1 |
| 2 |
∴∠PAO=90°,
∴∠POA=70°,
∴A、O、E、P四点在以OP为直径的圆上,
∴∠AEP=∠AOP=70°,
故选D.
点评:本题考查了切线的性质,垂径定理,四点共圆的判定以及圆周角定理,作出辅助线构建直角三角形以及证得A、O、E、P四点共圆本题是关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
下列运算正确的是( )
| A、-2(x-1)=-2x+2 |
| B、-2(x-1)=-2x-2 |
| C、-2(x-1)=-2x+1 |
| D、-2(x-1)=-2x-1 |
 已知a,b,c在数轴上的对应点如图所示,化简|a|-|a+b|+|c-a|+|b+c|.
已知a,b,c在数轴上的对应点如图所示,化简|a|-|a+b|+|c-a|+|b+c|.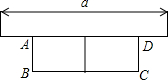 如图,有长为24米的篱笆,一边利用墙(墙的最大可用长度为3米),当花圃的宽AB为
如图,有长为24米的篱笆,一边利用墙(墙的最大可用长度为3米),当花圃的宽AB为 如图,在△ABC中,AC=BC,E是内心,AE的延长线交△ABC的外接圆于D.求证:
如图,在△ABC中,AC=BC,E是内心,AE的延长线交△ABC的外接圆于D.求证: