题目内容
5.一司机驾驶汽车从甲地去乙地,他以80km/h的平均速度,用6小时到达目的地.(1)当他按原路匀速返回时,汽车的速度v与时间t有怎样的函数关系?
(2)如果该司机必须在4个小时之内回到甲地,则返程时的速度不可能低于多少?
分析 (1)利用路程=平均速度×时间,进而得出汽车的速度v与时间t的函数关系;
(2)结合该司机必须在4个小时之内回到甲地,进而得出速度最小值.
解答 解:(1)由题意可得:两地路程有:80×6=480(km),
故汽车的速度v与时间t有怎样的函数关系为:v=$\frac{480}{t}$;
(2)由题意可得:4v≥480,
解得:v≥120.
答:返程时的速度不能低于120km/h.
点评 此题主要考查了反比例函数的应用,根据路程=平均速度×时间得出函数关系是解题关键.

练习册系列答案
 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案
相关题目
16.等腰三角形的底边长为5cm,一腰上的中线把周长分成的两部分之差为4cm,则腰长为( )
| A. | 1cm | B. | 9cm | C. | 1cm或9cm | D. | 以上都不对 |
17.在两个相似的五边形中,一个各边长分别为1、2、3、4、5,另一个最大边长为8,则后一个五边形的周长是( )
| A. | 27 | B. | 24 | C. | 21 | D. | 18 |




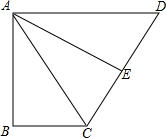 已知,如图,Rt△ABC中,∠B=90°,AB=6,BC=4,以斜边AC为底边作等腰三角形ACD,腰AD刚好满足AD∥BC,并作腰上的高AE.
已知,如图,Rt△ABC中,∠B=90°,AB=6,BC=4,以斜边AC为底边作等腰三角形ACD,腰AD刚好满足AD∥BC,并作腰上的高AE.