题目内容
20.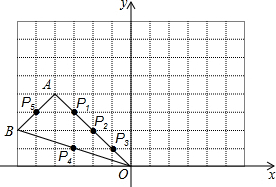 如图,在边长为1的小正方形组成的网格中,△AOB的顶点都在格点上,点A、B的坐标分别为(-4,4)、(-6,2).请按要求完成下列各题:
如图,在边长为1的小正方形组成的网格中,△AOB的顶点都在格点上,点A、B的坐标分别为(-4,4)、(-6,2).请按要求完成下列各题:(1)将△AOB绕点O顺时针旋转90°,画出旋转后的△A1OB1,在旋转过程中线段AO所扫过的面积为8π;
(2)点P1,P2,P3,P4,P5是△AOB边上的5个格点,画一个三角形,使它的三个顶点为P1,P2,P3,P4,P5中的3个格点并且与△AOB相似.(要求:在图中联结相应线段,不用说明理由)
分析 (1)根据图形旋转的性质画出旋转后的△A1OB1,由勾股定理求出OA的长,根据扇形的面积公式即可得出结论.
(2)利用△AOB各边的长度,利用相似三角形的性质得出答案.
解答 解:(1)如图1,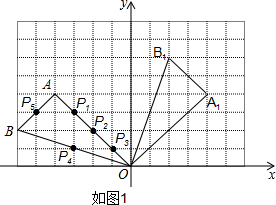
∵A的坐标为(-4,4)
∴OA=4$\sqrt{2}$
∴AO所扫过的面积=$\frac{1}{4}$πAO2=$\frac{1}{4}$π(4$\sqrt{2}$)2=8π;
故答案为:8π.
(2)如图2,△P2P4P5为所求三角形.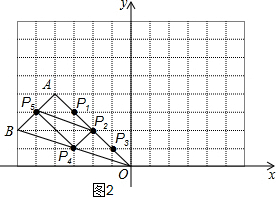
点评 本题考查的是作图-旋转变换,熟知图形旋转不变的性质是解答此题的关键.

练习册系列答案
相关题目
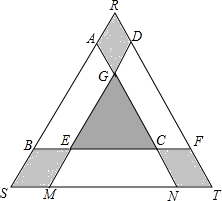 某学校矩形数学家“摇篮杯”会徽设计大赛,小明设计的会徽如图所示.正△DEF和正△GMN均由正△ABC平移得到,点A,B,M,N,F,D在正△RST边上,EC=2BE.若阴影部分的面积为$\frac{5\sqrt{3}}{32}$,则正△RST的边长是$\frac{5}{4}$.
某学校矩形数学家“摇篮杯”会徽设计大赛,小明设计的会徽如图所示.正△DEF和正△GMN均由正△ABC平移得到,点A,B,M,N,F,D在正△RST边上,EC=2BE.若阴影部分的面积为$\frac{5\sqrt{3}}{32}$,则正△RST的边长是$\frac{5}{4}$.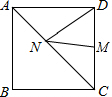 如图,在边长2正方形ABCD中,点M是CD的中点,在AC上确定点N,使DN+MN最小值是$\sqrt{5}$.
如图,在边长2正方形ABCD中,点M是CD的中点,在AC上确定点N,使DN+MN最小值是$\sqrt{5}$.