题目内容
3.已知关于x,y的方程组$\left\{\begin{array}{l}{\frac{3(x+1)}{2}+y=2}\\{3x-m=2y}\end{array}\right.$ 的解都不大于1,(1)求m的范围.
(2)化简:$\sqrt{{x}^{2}-2x+1}$+$\sqrt{{y}^{2}-2y+1}$+|m+3|+|m-5|-|x+y-2|
分析 (1)先求出方程组的解,得出关于m的不等式组,求出不等式组的解集即可;
(2)根据二次根式的性质和绝对值化简,再合并即可.
解答 解:(1)$\left\{\begin{array}{l}{\frac{3(x+1)}{2}+y=2}\\{3x-m=2y}\end{array}\right.$
整理得:$\left\{\begin{array}{l}{3x+2y=1①}\\{3x-2y=m②}\end{array}\right.$,
①+②得:6x=1+m,
解得:x=$\frac{1+m}{6}$,
①-②得:4y=1-m,
解得:y=$\frac{1-m}{4}$,
即方程组的解为$\left\{\begin{array}{l}{x=\frac{1+m}{6}}\\{y=\frac{1-m}{4}}\end{array}\right.$,
∵关于x,y的方程组$\left\{\begin{array}{l}{\frac{3(x+1)}{2}+y=2}\\{3x-m=2y}\end{array}\right.$ 的解都不大于1,
∴$\frac{1+m}{6}$≤1,且$\frac{1-m}{4}$≤1,
解得:-3≤m≤5;
(2)∵x=$\frac{1+m}{6}$≤1,y=$\frac{1-m}{4}$≤1,-3≤m≤5,
∴$\sqrt{{x}^{2}-2x+1}$+$\sqrt{{y}^{2}-2y+1}$+|m+3|+|m-5|-|x+y-2|
=|x-1|+|y-1|+|m+3|+|m-5|-|x+y-2|
=1-x+1-y+m+3+5-m+x+y-2
=8.
点评 本题考查了绝对值,解一元一次不等式组,二次根式的性质,解二元一次方程组,二元一次方程组的解的应用,解此题的关键是求出m的范围,比较典型,比较好.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案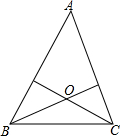 已知点O到△ABC的两边AB,AC所在直线的距离相等,且OB=OC,如图,若点O在△ABC的内部,求证:∠ABO=∠ACO.
已知点O到△ABC的两边AB,AC所在直线的距离相等,且OB=OC,如图,若点O在△ABC的内部,求证:∠ABO=∠ACO.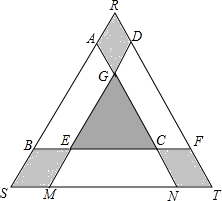 某学校矩形数学家“摇篮杯”会徽设计大赛,小明设计的会徽如图所示.正△DEF和正△GMN均由正△ABC平移得到,点A,B,M,N,F,D在正△RST边上,EC=2BE.若阴影部分的面积为$\frac{5\sqrt{3}}{32}$,则正△RST的边长是$\frac{5}{4}$.
某学校矩形数学家“摇篮杯”会徽设计大赛,小明设计的会徽如图所示.正△DEF和正△GMN均由正△ABC平移得到,点A,B,M,N,F,D在正△RST边上,EC=2BE.若阴影部分的面积为$\frac{5\sqrt{3}}{32}$,则正△RST的边长是$\frac{5}{4}$.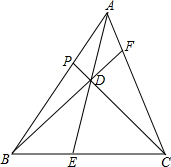 如图,在△ABC中,设E,F,P分别在边BC,CA,AB上,已知AE,BF,CP交于一点D,且$\frac{AD}{DE}$+$\frac{BD}{DF}$+$\frac{CD}{DP}$=n,则$\frac{AD}{DE}$$•\frac{BD}{DF}•\frac{CD}{DP}$=n+2.
如图,在△ABC中,设E,F,P分别在边BC,CA,AB上,已知AE,BF,CP交于一点D,且$\frac{AD}{DE}$+$\frac{BD}{DF}$+$\frac{CD}{DP}$=n,则$\frac{AD}{DE}$$•\frac{BD}{DF}•\frac{CD}{DP}$=n+2.