题目内容
7．
如图，梯形ABCD中，∠ADB=∠ACB=90°，AB∥DC，求证：AC=BD．
分析 根据∠ADB=∠ACB=90°，得到A、B、C、D四点共圆，得到∠CDB=∠CAB，∠DCA=∠DBA，根据平行线的性质和等腰三角形的判定定理证明即可．
解答 证明：
∵∠ADB=∠ACB=90°，
∴A、B、C、D四点共圆，
∴∠CDB=∠CAB，∠DCA=∠DBA，
∵AB∥DC，
∴∠CDB=∠ABD，∠DCA=∠CAB，
∴∠ABD=∠CAB，∠CAB=∠DBA，
∴OA=OB，OC=OD，
∴AC=BD．
点评 本题考查的是梯形的性质，掌握四点共圆的性质、平行线的性质、等腰三角形的判定定理是解题的关键．
练习册系列答案
芝麻开花课程新体验系列答案
相关题目
一个四边形的纸片ABCD，其中∠B=∠D=90°，把纸片按如图所示折叠，点B落在AD边上的E点，AF是折痕．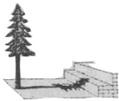
在阳光下，一名同学测得一根长为1米的垂直地面的竹竿的影长为0.6米，同时另一名同学测量树的高度时，发现树的影子不全落在地面上，有一部分落在教学楼的第一级台阶上，测得此影子长为0.2米，一级台阶高为0.3米，如图所示，若此时落在地面上的影长为4.42米，则树高为（ ）
如图，在梯形ABCD中，AD∥BC（AD＜BC），P为AD上一点，且∠BPC=∠A，求证：BP2=BC•AP．
如图，茬四边形ABCD中，AD∥BC，E是BC的中点，AC平分∠BCD，且AC⊥AB，接DE，交AC于F．
如图，在△ABC中，AC=BC，∠C=90°，AD是∠BAC的角平分线，DE⊥AB，垂足为E，若CD=2cm，则AC=2+$2\sqrt{2}$（cm）．