题目内容
 如图,AB是⊙O的直径,弦CD交AB于点E,∠ACD=62°,∠ADC=48°,则∠CEB的度数为
如图,AB是⊙O的直径,弦CD交AB于点E,∠ACD=62°,∠ADC=48°,则∠CEB的度数为考点:圆周角定理
专题:
分析:连接BC,由AB是⊙O的直径,则∠ACB=90°,而∠ABC=∠D=48°,可得∠BAC=42°,然后利用三角形外角的性质可求出∠CEB=∠BAC+∠C=42°+62°=104°.
解答:
 解:连接BC.
解:连接BC.
∵AB是⊙O的直径,
∴∠ACB=90°,
∴∠BAC+∠ABC=90°.
∵∠ABC=∠ADC=48°
∴∠BAC=90°-∠ABC=90°-48°=42°.
∴∠CEB=∠BAC+∠ACD=42°+62°=104°.
故答案为:104°.
 解:连接BC.
解:连接BC.∵AB是⊙O的直径,
∴∠ACB=90°,
∴∠BAC+∠ABC=90°.
∵∠ABC=∠ADC=48°
∴∠BAC=90°-∠ABC=90°-48°=42°.
∴∠CEB=∠BAC+∠ACD=42°+62°=104°.
故答案为:104°.
点评:本题考查了圆周角定理.在同圆或等圆中,同弧和等弧所对的圆周角相等,一条弧所对的圆周角是它所对的圆心角的一半.也考查了直径所对的圆周角为90度和三角形的外角性质.

练习册系列答案
 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案
相关题目
如图所示,给出下列四组条件:①AB=DE,BC=EF,AC=DF;②∠A=∠D;∠B=∠E,∠C=∠F;③AB=DE,BC=EF,∠B=∠E;④AB=DE,∠C=∠F,AC=DF.其中能使△ABC≌△DEF的条件的组数共有( )
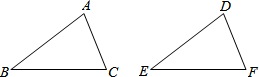

| A、1组 | B、2组 | C、3组 | D、4组 |
若a、b互为相反数,c、d互为倒数,|m|=2,则代数式m2-3cd+
的值为( )
| a+b |
| m |
| A、-1 | B、1 | C、-7 | D、1或-7 |
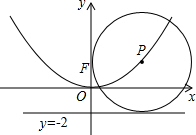 如图,在平面直角坐标系xOy中,若动点P在抛物线y=ax2上,⊙P恒过点F(0,2),且与直线y=-2始终保持相切,则a=
如图,在平面直角坐标系xOy中,若动点P在抛物线y=ax2上,⊙P恒过点F(0,2),且与直线y=-2始终保持相切,则a=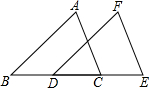 如图,△ABC沿直线l向右移了3厘米,得△FDE,且BC=6厘米,∠B=40°.
如图,△ABC沿直线l向右移了3厘米,得△FDE,且BC=6厘米,∠B=40°.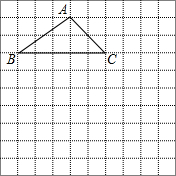 如图所示,在10×10正方形网格中,△ABC的三个顶点都在格点上,请按下列要求画图并回答问题:
如图所示,在10×10正方形网格中,△ABC的三个顶点都在格点上,请按下列要求画图并回答问题: 如图,已知点P是二次函数y=-x2+3x图象在y轴右侧部分上的一个动点,将直线y=-2x,沿y轴向上平移,分别交x轴,y轴于C、D两点.CD⊥CP,且CD=2CP,求点P的坐标.
如图,已知点P是二次函数y=-x2+3x图象在y轴右侧部分上的一个动点,将直线y=-2x,沿y轴向上平移,分别交x轴,y轴于C、D两点.CD⊥CP,且CD=2CP,求点P的坐标.