Question

18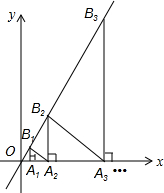．如图，在坐标轴上取点A₁（2，0），作x轴的垂线与直线y=2x交于点B₁，作等腰直角三角形A₁B₁A₂；又过点A₂作x轴的垂线交直线y=2x交于点B₂，作等腰直角三角形A₂B₂A₃；…，如此反复作等腰直角三角形，当作到A_n（n为正整数）点时，则A_n的坐标是（2×3^n-1，0）．

Answer 1

分析 根据直线OB_n的解析式以及等腰直角三角形的性质即可得出部分线段A_nB_n的长，根据长度的变化即可找出变化规律“A_nB_n=4×3^n-1（n为正整数）”，再根据OA_n=$\frac{1}{2}$A_nB_n，即可得出点A_n的坐标．

解答 解：∵点B₁、B₂、B₃、…、B_n在直线y=2x的图象上，
∴A₁B₁=4，A₂B₂=2×（2+4）=12，A₃B₃=2×（2+4+12）=36，A₄B₄=2×（2+4+12+36）=108，…，
∴A_nB_n=4×3^n-1（n为正整数）．
∵OA_n=$\frac{1}{2}$A_nB_n，
∴点A_n的坐标为（2×3^n-1，0）．
故答案为：（2×3^n-1，0）．

点评 本题考查了一次函数图象上点的坐标特征、等腰直角三角形的性质以及规律型中点的坐标，解题的关键是找出线段A_nB_n的变化规律“A_nB_n=4×3^n-1（n为正整数）”．本题属于中档题，难度不大，解决该题型题目时，结合一次函数图象上点的坐标特征以及等腰直角三角形的性质找出线段的变化规律是关键．