Question

7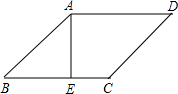．如图，在菱形ABCD中，AE⊥BC于E，EC=2，tanB=$\frac{5}{12}$，求菱形的边长．

Answer 1

分析 首先设菱形ABCD的边长为x，由AE⊥BC，tanB=$\frac{5}{12}$，可求得cosB=$\frac{12}{13}$，继而可得方程：$\frac{x-2}{x}$=$\frac{12}{13}$，解此方程即可求得答案．

解答 解：设菱形ABCD的边长为x，
则AB=BC=x，
∵EC=2，
∴BE=BC-EC=x-2，
∵AE⊥BC，tanB=$\frac{5}{12}$，
∴cosB=$\frac{12}{13}$，
∵cosB=$\frac{BE}{AB}$，
∴$\frac{x-2}{x}$=$\frac{12}{13}$，
解得：x=26．
∴菱形的边长为：26．

点评 此题考查了菱形的性质以及三角函数的应用．注意利用方程思想求解是解此题的关键．