题目内容
14.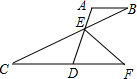 如图AB∥CD,AD与BC交于点E,EF平分∠BED交CD延长线于点F,若∠A=110°,∠B=30°,则∠F的度数是( )
如图AB∥CD,AD与BC交于点E,EF平分∠BED交CD延长线于点F,若∠A=110°,∠B=30°,则∠F的度数是( )| A. | 20° | B. | 30° | C. | 40° | D. | 50° |
分析 首先根据三角形的外角的性质求得∠BED的度数,则∠DEF即可求得,根据平行线的性质∠CDE=∠A=110°,然后在△DEF中利用三角形的外角的性质求得∠F的度数.
解答 解:∠BED=∠B+∠A=110°+30°=140°.
∵EF平分∠BED,
∴∠DEF=$\frac{1}{2}$∠BED=70°.
∵AB∥CD,
∴∠CDE=∠A=110°,
又∵∠CDE=∠F+∠DEF,
∴∠F=∠CDE-∠DEF=110°-70°=40°.
故选C.
点评 本题考查了平行线的性质以及三角形的外角等于不相邻的两个内角的和,理解定理是关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
5.已知一个多项式是三次二项式,则这个多项式可以是( )
| A. | x2-2x+1 | B. | 2x3+1 | C. | x2-2x | D. | x3-2x2+1 |
9.对于双曲线y=$\frac{1-m}{x}$,当x>0时,y随x的增大而减小,则m的取值范围为( )
| A. | m>0 | B. | m>1 | C. | m<0 | D. | m<1 |
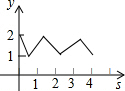
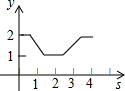
 如图,在平面直角坐标系中,边长为1的正方形ABCD中,AD边的中点处有一动点P,动点P沿P→D→C→B→A→P运动一周,则P点的纵坐标y与点P走过的路程s之间的函数关系用图象表示大致是( )
如图,在平面直角坐标系中,边长为1的正方形ABCD中,AD边的中点处有一动点P,动点P沿P→D→C→B→A→P运动一周,则P点的纵坐标y与点P走过的路程s之间的函数关系用图象表示大致是( )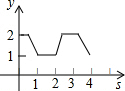
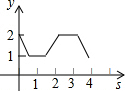
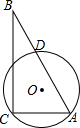 如图,直角△ABC的直角顶点C,另一顶点A及斜边AB的中点D都在⊙O上,已知:AC=6,BC=8,则⊙O的半径为$\frac{25}{8}$.
如图,直角△ABC的直角顶点C,另一顶点A及斜边AB的中点D都在⊙O上,已知:AC=6,BC=8,则⊙O的半径为$\frac{25}{8}$.