题目内容
2.有三张大小一样而画面不同的画片,先将每一张从中间剪开,分成上下两部分;然后把三张画片的上半部分都放在第一个盒子中,把下半部分都放在第二个盒子中.分别摇匀后,从每个盒子中各随机地摸出一张,则这两张恰好能拼成原来的一幅画的概率为$\frac{1}{3}$.分析 用A、a表示第1张的上下部分,用B、b表示第2张的上下部分,用C、c表示第3张的上下部分,画树状图展示所有9种等可能的结果数,再找出这两张恰好能拼成原来的一幅画的结果数,然后根据概率公式求解.
解答 解:用A、a表示第1张的上下部分,用B、b表示第2张的上下部分,用C、c表示第3张的上下部分,
画树状图为:
共有9种等可能的结果数,其中这两张恰好能拼成原来的一幅画的结果数为3,
所以这两张恰好能拼成原来的一幅画的概率=$\frac{3}{9}$=$\frac{1}{3}$.
故答案为$\frac{1}{3}$.
点评 本题考查了列表法与树状图法:通过列表法或树状图法展示所有等可能的结果求出n,再从中选出符合事件A或B的结果数目m,然后根据概率公式求出事件A或B的概率.利用字母表示画片使解决问题时简便.

练习册系列答案
相关题目
12.已知等腰三角形的一个内角为70°,则另外两个角的度数为( )
| A. | 55°,55° | B. | 55°,70° | ||
| C. | 70°,40° | D. | 55°,55°或70°,40° |
13.计算(-5)÷(-2)=( )
| A. | -$\frac{5}{2}$ | B. | -$\frac{2}{5}$ | C. | $\frac{5}{2}$ | D. | $\frac{2}{5}$ |
10.下列各式计算正确的是( )
| A. | a3•a=a4 | B. | 2a3+a3=3a6 | C. | (-a2b)3=a6b3 | D. | (b+2a)(2a-b)=b2-4a2 |
7.下列运算正确的是( )
| A. | a•a2=a3 | B. | 3a+2a2=5a2 | C. | 2-3=-8 | D. | $\sqrt{9}$=±3 |
14.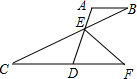 如图AB∥CD,AD与BC交于点E,EF平分∠BED交CD延长线于点F,若∠A=110°,∠B=30°,则∠F的度数是( )
如图AB∥CD,AD与BC交于点E,EF平分∠BED交CD延长线于点F,若∠A=110°,∠B=30°,则∠F的度数是( )
 如图AB∥CD,AD与BC交于点E,EF平分∠BED交CD延长线于点F,若∠A=110°,∠B=30°,则∠F的度数是( )
如图AB∥CD,AD与BC交于点E,EF平分∠BED交CD延长线于点F,若∠A=110°,∠B=30°,则∠F的度数是( )| A. | 20° | B. | 30° | C. | 40° | D. | 50° |
 据PM2.5监测网数据:嘉兴市实时空气质量指数(AQI)显示,嘉兴市4月份中一周空气质量指数数据如下图,则其中位数是77.
据PM2.5监测网数据:嘉兴市实时空气质量指数(AQI)显示,嘉兴市4月份中一周空气质量指数数据如下图,则其中位数是77.
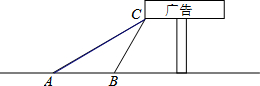 如图,某学校数学兴趣小组想了解“第25届世界技巧锦标赛倒计时”广告牌的高度,他们在A点处测得广告牌底端C点的仰角为30°,然后向广告牌前进10m到达点B处,又测得C点的仰角为60°.请你根据以上数据求广告牌底端C点离地面的高度.(结果保留根号)
如图,某学校数学兴趣小组想了解“第25届世界技巧锦标赛倒计时”广告牌的高度,他们在A点处测得广告牌底端C点的仰角为30°,然后向广告牌前进10m到达点B处,又测得C点的仰角为60°.请你根据以上数据求广告牌底端C点离地面的高度.(结果保留根号)