题目内容
10.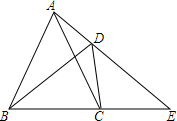 已知,如图,在四边形ABCD中,∠ADB=∠ACB,延长AD、BC相交于点E.求证:
已知,如图,在四边形ABCD中,∠ADB=∠ACB,延长AD、BC相交于点E.求证:(1)△ACE∽△BDE;
(2)BE•DC=AB•DE.
分析 (1)根据邻补角的定义得到∠BDE=∠ACE,即可得到结论;
(2)根据相似三角形的性质得到$\frac{BE}{AE}=\frac{ED}{EC}$,由于∠E=∠E,得到△ECD∽△EAB,由相似三角形的性质得到$\frac{AE}{EC}=\frac{AB}{CD}$,等量代换得到$\frac{BE}{ED}=\frac{AB}{CD}$,即可得到结论.
解答 证明:(1)∵∠ADB=∠ACB,
∴∠BDE=∠ACE,
∴△ACE∽△BDE;
(2)∵△ACE∽△BDE,
∴$\frac{BE}{AE}=\frac{ED}{EC}$,
∵∠E=∠E,
∴△ECD∽△EAB,
∴$\frac{AE}{EC}=\frac{AB}{CD}$,
∴$\frac{BE}{ED}=\frac{AB}{CD}$,
∴BE•DC=AB•DE.
点评 本题考查了相似三角形的判定和性质,邻补角的定义,熟练掌握相似三角形的判定和性质是解题的关键.

练习册系列答案
 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南大学出版社系列答案
同步练习西南大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目
 如图,D为△ABC的边BC的中点,F为AC边上的点,AF=$\frac{1}{2}$FC,BF交AD于点E.求证:点E为AD的中点.
如图,D为△ABC的边BC的中点,F为AC边上的点,AF=$\frac{1}{2}$FC,BF交AD于点E.求证:点E为AD的中点. 已知,如图,四边形ABCD中,AB=3cm,AD=4cm,BC=13cm,CD=12cm,且∠A=90°.求证:△BCD是直角三角形.
已知,如图,四边形ABCD中,AB=3cm,AD=4cm,BC=13cm,CD=12cm,且∠A=90°.求证:△BCD是直角三角形.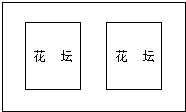 某中学为了美化校园,决定在一个长是宽1.5倍的矩形空地中间修建两个全等的矩形花坛(如图所示),在空白的地带修建宽都为2米的花径,花径的面积占整个空地面积的$\frac{9}{25}$,求这块空地的长为多少米?
某中学为了美化校园,决定在一个长是宽1.5倍的矩形空地中间修建两个全等的矩形花坛(如图所示),在空白的地带修建宽都为2米的花径,花径的面积占整个空地面积的$\frac{9}{25}$,求这块空地的长为多少米?