题目内容
19.联系(-2)2、22、(-2)3、23,这类具体数的乘方,当a<0时,下列各式正确的个数有( )个.①a2>0;②a2=(-a)2;③a3>0;④a3=-a3.
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 依据有理数的乘法法则进行判断即可.
解答 解:①当a<0时,不①成立,②成立;③当a≤0时,不成立,④当a>0或a<0时,不成立,故正确的只有②.
故选:B.
点评 本题主要考查的是有理数的乘方,掌握有理数的乘法法则是解题的关键.

练习册系列答案
相关题目
9.下列是一元二次方程的是( )
| A. | (x+1)(x-1)=x2-x | B. | ${x^2}-\frac{1}{x}=0$ | C. | ax2+bx+c=0 | D. | x2=0 |
7.根据下列条件不能唯一画出△ABC的是( )
| A. | AB=5,BC=6,AC=7 | B. | AB=5,BC=6,∠B=45° | ||
| C. | AB=5,AC=4,∠C=90° | D. | AB=5,AC=4,∠C=45° |
11.已知α和β是一元二次方程x2+2x-6=0的两根,则α2+β2=( )
| A. | 16 | B. | 8 | C. | -8 | D. | 12 |
9.将抛物线y=$\frac{1}{2}$x2-6x+21绕原点旋转180°后,所得新抛物线的解析式为( )
| A. | y=$\frac{1}{2}$x2+6x+21 | B. | y=-$\frac{1}{2}$x2+6x-21 | C. | y=-$\frac{1}{2}$x2-6x+21 | D. | y=-$\frac{1}{2}$x2-6x-21 |
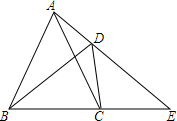 已知,如图,在四边形ABCD中,∠ADB=∠ACB,延长AD、BC相交于点E.求证:
已知,如图,在四边形ABCD中,∠ADB=∠ACB,延长AD、BC相交于点E.求证: