题目内容
1. 已知,如图,四边形ABCD中,AB=3cm,AD=4cm,BC=13cm,CD=12cm,且∠A=90°.求证:△BCD是直角三角形.
已知,如图,四边形ABCD中,AB=3cm,AD=4cm,BC=13cm,CD=12cm,且∠A=90°.求证:△BCD是直角三角形.
分析 首先利用勾股定理计算出BD长,再利用勾股定理逆定理证明∠BDC=90°,可得△BCD是直角三角形.
解答 证明:∵AB=3cm,AD=4cm,∠A=90°,
∴BD=$\sqrt{{3}^{2}+{4}^{2}}$=5(cm),
∵52+122=132,
∴BD2+CD2=BC2,
∴∠BDC=90°,
∴△BCD是直角三角形.
点评 此题主要考查了勾股定理和勾股定理逆定理,关键是掌握如果三角形的三边长a,b,c满足a2+b2=c2,那么这个三角形就是直角三角形.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
18.某班52名师生准备全部去亮子河旅游,为确定旅游费用,班主任刘老师派班长去了解船只租金情况,班长得到如下表格:
(1)若单租A型船或B型船,至少需多少只?
(2)如果两种船都租,且既不超载也不空载,那么你能设计出几种租船方案?
(3)若你是班长,使总租金最少,应该选择怎样的租船方案?
| A型 | B型 | |
| (人/只) | 5 | 3 |
| (元/只) | 160 | 105 |
(2)如果两种船都租,且既不超载也不空载,那么你能设计出几种租船方案?
(3)若你是班长,使总租金最少,应该选择怎样的租船方案?
9.下列是一元二次方程的是( )
| A. | (x+1)(x-1)=x2-x | B. | ${x^2}-\frac{1}{x}=0$ | C. | ax2+bx+c=0 | D. | x2=0 |
11.已知α和β是一元二次方程x2+2x-6=0的两根,则α2+β2=( )
| A. | 16 | B. | 8 | C. | -8 | D. | 12 |
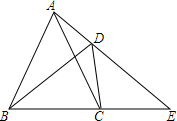 已知,如图,在四边形ABCD中,∠ADB=∠ACB,延长AD、BC相交于点E.求证:
已知,如图,在四边形ABCD中,∠ADB=∠ACB,延长AD、BC相交于点E.求证: