题目内容
9.(1)如图1,在△ABC中,O是∠ABC与∠ACB的平分线BO和CO的交点,若∠A=50°,求∠BOC的度数.(2)如图2中,O是∠ABC与外角∠ACD的平分线BO和CO的交点,试分析∠BOC与∠A有怎样的关系?请说明理由.

分析 (1)根据三角形内角和定理求出∠ABC+∠ACB=130°,根据角平分线定义求出∠OBC+∠OCB,根据三角形内角和定理求出即可;
(2)利用角平分线的性质与外角的性质得出∠2=$\frac{1}{2}$∠A+∠1,∠BOC=∠2-∠1,然后整理即可得到∠BOC与∠A的关系.
解答 解:(1)∵∠A=50°,
∴∠ABC+∠ACB=180°-50°=130°,
∵∠ABC的平分线与∠ACB的平分线相交于点O,
∴∠OBC+∠OCB=$\frac{1}{2}$(∠ABC+∠ACB)=65°,
∴∠BOC=180°-(∠OBC+∠OCB)=115°;
(2)∠BOC=$\frac{1}{2}$∠A,
理由: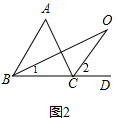 如图2,
如图2,
∵BO和CO分别是∠ABC和∠ACD的角平分线,
∴∠1=$\frac{1}{2}$∠ABC,∠2=$\frac{1}{2}$∠ACD,
又∵∠ACD是△ABC的一外角,
∴∠ACD=∠A+∠ABC,
∴∠2=$\frac{1}{2}$(∠A+∠ABC)=$\frac{1}{2}$∠A+∠1,
∵∠2是△BOC的一外角,
∴∠BOC=∠2-∠1=$\frac{1}{2}$∠A+∠1-∠1=$\frac{1}{2}$∠A.
点评 本题考查了三角形的外角性质与内角和定理,熟记三角形的一个外角等于与它不相邻的两个内角的和是解题的关键.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案
相关题目
18.现有数学、木工和音乐三个专业,甲,乙,丙三位同学各喜欢其中一个,且喜欢的专业互不相同.已知他们的特征如下:
①丙是女生,她的年龄最小;
②甲讨厌木材和铁钉;
③本校只有男生才喜欢木工;
④喜欢音乐的同学年龄最大.
则喜欢数学的同学是( )
①丙是女生,她的年龄最小;
②甲讨厌木材和铁钉;
③本校只有男生才喜欢木工;
④喜欢音乐的同学年龄最大.
则喜欢数学的同学是( )
| A. | 甲 | B. | 乙 | C. | 丙 | D. | 无法判断 |
19.从2种不同款式的衬衣和2种不同款式的裙子中分别取一件衬衣和一条裙子搭配,有( )种可能.
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
 已知:AB⊥BC于B,CD⊥BC于C,AB=4,CD=6,BC=14,点P在BD上移动,当以P,C,D为顶点的三角形与△ABP相似时,求PB的长?
已知:AB⊥BC于B,CD⊥BC于C,AB=4,CD=6,BC=14,点P在BD上移动,当以P,C,D为顶点的三角形与△ABP相似时,求PB的长?