题目内容
7.(1)解方程组$\left\{\begin{array}{l}{3(x-1)=y+5}\\{5(y-1)=3(x+5)}\end{array}\right.$(2)解不等式组$\left\{\begin{array}{l}{2x+4≤3(x+2)}\\{2x-\frac{1+3x}{2}<1}\end{array}\right.$.
分析 (1)将方程组整理成一般式,利用加减消元法可得方程组的解;
(2)分别求出每一个不等式的解集,根据口诀:同大取大、同小取小、大小小大中间找、大大小小无解了确定不等式组的解集.
解答 解:(1)整理得:
$\left\{\begin{array}{l}{3x-y=8}\\{3x-5y=-20}\end{array}\right.$
①-②得:4y=28,
解得:y=7,
把y=7代入①得,3x-7=8,
解得:x=5
所以,原方程组的解为:$\left\{\begin{array}{l}{x=5}\\{y=7}\end{array}\right.$;
(2)解不等式组:$\left\{\begin{array}{l}{2x+4≤3(x+5)}&{①}\\{2x-\frac{1+3x}{2}<1}&{②}\end{array}\right.$
解不等式①得,x≥-2,
解不等式②得,x<3,
所以不等式组的解集为:-2≤x<3.
点评 本题考查的是解方程组和一元一次不等式组的能力,消元的思想是解多元方程的根本,正确求出每一个不等式解集是基础,熟知“同大取大;同小取小;大小小大中间找;大大小小找不到”的原则是解答此题的关键.

练习册系列答案
 全优点练单元计划系列答案
全优点练单元计划系列答案
相关题目
19.数字$\sqrt{2}$、$\frac{1}{3}$,π,$\root{3}{8}$,0.$\stackrel{•}{3}\stackrel{•}{2}$中无理数的个数有多少个( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
17.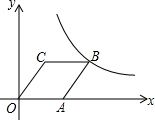 如图,菱形OABC的顶点C的坐标为(1,$\sqrt{3}$),顶点A在x轴的正半轴上,反比例函数y=$\frac{k}{x}$(x>0)的图象经过顶点B,则k的值为( )
如图,菱形OABC的顶点C的坐标为(1,$\sqrt{3}$),顶点A在x轴的正半轴上,反比例函数y=$\frac{k}{x}$(x>0)的图象经过顶点B,则k的值为( )
 如图,菱形OABC的顶点C的坐标为(1,$\sqrt{3}$),顶点A在x轴的正半轴上,反比例函数y=$\frac{k}{x}$(x>0)的图象经过顶点B,则k的值为( )
如图,菱形OABC的顶点C的坐标为(1,$\sqrt{3}$),顶点A在x轴的正半轴上,反比例函数y=$\frac{k}{x}$(x>0)的图象经过顶点B,则k的值为( )| A. | 2+$\sqrt{3}$ | B. | 3+$\sqrt{3}$ | C. | 2$\sqrt{3}$ | D. | 3$\sqrt{3}$ |
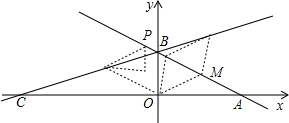 如图,直线y=kx+b的图象分别交x轴、y轴于点A,B,且OA,OB的长是方程x(6-x)=8的两个根(OA>OB),点C在x轴的负半轴上,tan∠BCA=$\frac{1}{3}$,M是AB的中点.
如图,直线y=kx+b的图象分别交x轴、y轴于点A,B,且OA,OB的长是方程x(6-x)=8的两个根(OA>OB),点C在x轴的负半轴上,tan∠BCA=$\frac{1}{3}$,M是AB的中点.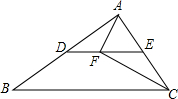 如图,在△ABC中,∠ACB=56°,点D,E分别是AB,AC的中点.若点F在线段DE上,且∠AFC=90°,则∠FAE的度数为62°.
如图,在△ABC中,∠ACB=56°,点D,E分别是AB,AC的中点.若点F在线段DE上,且∠AFC=90°,则∠FAE的度数为62°.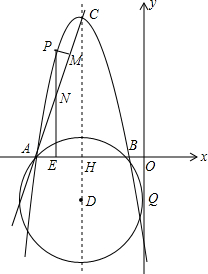 在平面直角坐标系中,以D(-4,$\sqrt{7}$)为圆心的⊙D与y轴相切于点Q,与x轴交于A、B两点,其中点B坐标为(-1,0).以CD为对称轴的抛物线与⊙D交于A、B两点,点C坐标为(-4,9).CD与x轴交于点H
在平面直角坐标系中,以D(-4,$\sqrt{7}$)为圆心的⊙D与y轴相切于点Q,与x轴交于A、B两点,其中点B坐标为(-1,0).以CD为对称轴的抛物线与⊙D交于A、B两点,点C坐标为(-4,9).CD与x轴交于点H