题目内容
6.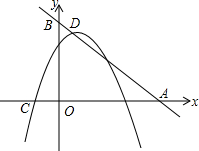 如图,直线y=-x+5与x、y轴分别交于点A、B,抛物线y=-x2+bx+c的顶点在直线AB上,且经过另一点(2,3)
如图,直线y=-x+5与x、y轴分别交于点A、B,抛物线y=-x2+bx+c的顶点在直线AB上,且经过另一点(2,3)(1)求抛物线的解析式.
(2)设抛物线与x轴的负半轴交于点C,在直线y=-x+5有一点E,使△ABO与△ACE相似,求出点E的坐标.
(3)在(2)的条件下,在x轴下方的抛物线上,是否存在点P,使△APC的面积等于△ACE的面积?如果存在,请求出点P的坐标;如果不存在,请说明理由.
分析 (1)设抛物线的顶点坐标为(t,-t+5),利用顶点式得到y=-(x-t)2-t+5,然后把(2,3)代入求出t的值即可得到抛物线解析式;
(2)根据坐标轴上点的坐标特征确定B(0,5)、A(5,0),C(-1,0),则可判断△AOB为等腰直角三角形,所以∠BAO=45°,然后分类讨论:作CF⊥AB于F,如图1,则△ACE为等腰直角三角形,所以△AOB∽△ACE,根据等腰直角三角形的性质得EF=$\frac{1}{2}$AC=3,于是得到E点坐标为(2,3);过点C作CE⊥x轴交直线y=-x+5于E点,如图2,易得E(-1,6),可证明△AOB∽△ACE;
(3)设P(x,-x2+2x+3),分类讨论:当E(2,3)时,利用三角形面积公式得到$\frac{1}{2}$•6•(x2-2x-3)=9,解得x1=1+$\sqrt{7}$,x2=1-$\sqrt{7}$,于是得到P点坐标为(1+$\sqrt{7}$,-3)或(1-$\sqrt{7}$,-3);当E(-1,6)时,利用三角形面积公式得到$\frac{1}{2}$•6•(x2-2x-3)=18,解得x1=1+$\sqrt{10}$,x2=1-$\sqrt{10}$,于是得到P点坐标为(1+$\sqrt{10}$,-6)或(1-$\sqrt{10}$,-6).
解答 解:(1)设抛物线的顶点坐标为(t,-t+5),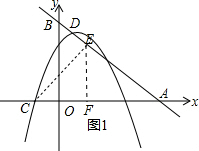
则抛物线解析式为y=-(x-t)2-t+5,
把(2,3)代入得-(2-t)2-t+5=3,
整理得t2-3t+2=0,解得t1=1,t2=2(舍去),
所以抛物线解析式为y=-(x-1)2-1+5,即y=-x2+2x+3;
(2)当x=0时,y=-x+5=5,则B(0,5);当y=0时,-x+5=0,解得x=5,则A(5,0),
当y=0时,-x2+2x+3,解得x1=1,x2=3,则C(-1,0),
∵OA=OB=5,
∴△AOB为等腰直角三角形,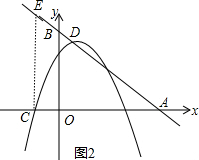
∴∠BAO=45°,
作CF⊥AB于F,如图1,则△ACE为等腰直角三角形,△AOB∽△ACE,
∴EF=$\frac{1}{2}$AC=$\frac{1}{2}$(5+1)=3,
∴E点坐标为(2,3),
过点C作CE⊥x轴交直线y=-x+5于E点,如图2,当x=-1时,y=-x+5=6,则E(-1,6),
∵CE∥OB,
∴△AOB∽△ACE,
综上所述,点E的坐标为(-1,6)或(2,3);
(3)存在.
设P(x,-x2+2x+3),
当E(2,3)时,S△ACE=$\frac{1}{2}$×6×3=9,
∵△APC的面积等于△ACE的面积,
∴$\frac{1}{2}$•6•(x2-2x-3)=9,解得x1=1+$\sqrt{7}$,x2=1-$\sqrt{7}$,
此时P点坐标为(1+$\sqrt{7}$,-3)或(1-$\sqrt{7}$,-3);
当E(-1,6)时,S△ACE=$\frac{1}{2}$×6×6=18,
∵△APC的面积等于△ACE的面积,
∴$\frac{1}{2}$•6•(x2-2x-3)=18,解得x1=1+$\sqrt{10}$,x2=1-$\sqrt{10}$,
此时P点坐标为(1+$\sqrt{10}$,-6)或(1-$\sqrt{10}$,-6).
点评 本题考查了二次函数的综合题:熟练掌握二次函数图形上点的坐标特征和求二次函数解析式;理解坐标与图形性质,记住三角形的面积公式;会灵活运用等腰直角三角形的性质;会运用分类讨论思想解决数学问题.


 如图,△ABC中,$\frac{DC}{DB}$=$\frac{EA}{EC}$=$\frac{FB}{FA}$=$\frac{1}{2}$,求$\frac{△GHI的面积}{△ABC的面积}$的值.
如图,△ABC中,$\frac{DC}{DB}$=$\frac{EA}{EC}$=$\frac{FB}{FA}$=$\frac{1}{2}$,求$\frac{△GHI的面积}{△ABC的面积}$的值.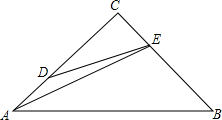 如图,已知△ABC,∠ACB=90°,AC=BC,点D在AC上,点E在BC上,AD=CE,CD=2AD,求证:∠CDE=∠EAB.
如图,已知△ABC,∠ACB=90°,AC=BC,点D在AC上,点E在BC上,AD=CE,CD=2AD,求证:∠CDE=∠EAB.