题目内容
5. 如图,在平面直角坐标系中,已知B(8,0),C(0.6),P(-3,3),现将一直角三角板EPF的直角顶点放在点P处,EP交y轴于N,FP交x轴于M,把△EPF绕点P旋转,请问0M+ON是否为一定值?若是,求出其值;若不是,请说明理由.
如图,在平面直角坐标系中,已知B(8,0),C(0.6),P(-3,3),现将一直角三角板EPF的直角顶点放在点P处,EP交y轴于N,FP交x轴于M,把△EPF绕点P旋转,请问0M+ON是否为一定值?若是,求出其值;若不是,请说明理由.
分析 作PG⊥x轴于G,PH⊥y轴于H,得到矩形PGOH,根据矩形的性质和全等三角形的判定定理证明△NPH≌△MPG,得到NH=MG,根据图形的性质得到答案.
解答  解:0M+ON为一定值6,
解:0M+ON为一定值6,
理由如下:作PG⊥x轴于G,PH⊥y轴于H,
∴四边形PGOH为矩形,
∴∠HPG=90°,又∠EPF=90°,
∴∠NPH=∠MPG,
∵P(-3,3),
∴PH=PG=3,
在△NPH和△MPG中,
$\left\{\begin{array}{l}{∠NPH=∠MPG}\\{PH=PG}\\{∠NHP=∠MGP}\end{array}\right.$,
∴△NPH≌△MPG,
∴NH=MG,
∴0M+ON=OG+OH=6.
点评 本题考查的是坐标与图形的性质、确定三角形的判定和性质,正确作出辅助线、构造全等三角形是解题的关键.

练习册系列答案
相关题目
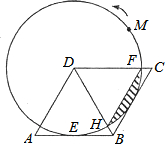 如图,在菱形ABCD中,AB=2$\sqrt{3}$,∠A=60°,以点D为圆心的⊙D与边AB相切于点E.
如图,在菱形ABCD中,AB=2$\sqrt{3}$,∠A=60°,以点D为圆心的⊙D与边AB相切于点E.
