题目内容
16. (1)先化简,再求值(2x+3)(2x-3)-4x(x-1)+(x+2)2,其中x=3.
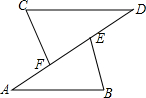
(1)先化简,再求值(2x+3)(2x-3)-4x(x-1)+(x+2)2,其中x=3.(2)已知如图:AB∥CD,EB∥FC,AF=DE.求证:△ABE≌△DCF.
分析 (1)先算乘法,再合并同类项,最后代入求出即可;
(2)求出AE=DF,根据平行线的性质求出∠A=∠D,∠AEB=∠DFC,根据ASA推出即可.
解答 (1)解:原式=4x2-9-4x2+4x+x2+4x+4
=8x-5,
当x=3时,原式=8x-5=19;
(2)证明:∵AF=DE,
∴AE=DF
∵AB∥CD,EB∥FC,
∴∠A=∠D,∠AEB=∠DFC,
在△ABE和△DCF中
$\left\{\begin{array}{l}{∠A=∠D}\\{AE=DF}\\{∠BEA=∠CFD}\end{array}\right.$
∴△ABE≌△DCF(ASA).
点评 本题考查了整式的混合运算和求值,平行线的性质,全等三角形的判定的应用,能正确进行化简是解(1)小题的关键,能求出判定两三角形全等的三个条件是解(2)小题的关键.

练习册系列答案
相关题目
4.在平面直角坐标系中,点A(-2,-3)在( )象限.
| A. | 一 | B. | 二 | C. | 三 | D. | 四 |
1.一种面粉的质量标识为“28±0.25千克”,则下列面粉中合格的是( )
| A. | 28.30千克 | B. | 27.70千克 | C. | 28.51千克 | D. | 27.80千克 |
 如图,在△ABC中,DE∥BC,若AD=1,DE=2,AB=4,则BC=8.
如图,在△ABC中,DE∥BC,若AD=1,DE=2,AB=4,则BC=8. 如图,在△ABC中,AB=AC,D是AC上的一点,CD=9,BC=15,BD=12.
如图,在△ABC中,AB=AC,D是AC上的一点,CD=9,BC=15,BD=12.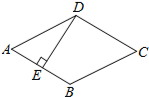 如图,菱形ABCD中,E是AB中点,DE⊥AB,则∠ADC的度数为120°.
如图,菱形ABCD中,E是AB中点,DE⊥AB,则∠ADC的度数为120°. 如图,梯形ABCD中,DC∥EF∥AB,AC交EF于G.若AE=2ED,CF=2cm,那么CB的长是多少?
如图,梯形ABCD中,DC∥EF∥AB,AC交EF于G.若AE=2ED,CF=2cm,那么CB的长是多少? 作图:在∠AOB内找一点P,使点到角两边距离相等,不写作法但要保留作图痕迹.
作图:在∠AOB内找一点P,使点到角两边距离相等,不写作法但要保留作图痕迹.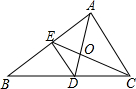 如图,在△ABC中,D、E分别为边BC、AB的中点,AD、CE相交于O,AB=8,BC=10,AC=6,求OD=$\frac{5}{3}$.
如图,在△ABC中,D、E分别为边BC、AB的中点,AD、CE相交于O,AB=8,BC=10,AC=6,求OD=$\frac{5}{3}$.