题目内容
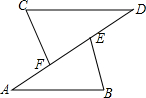
8．
如图，梯形ABCD中，DC∥EF∥AB，AC交EF于G．若AE=2ED，CF=2cm，那么CB的长是多少？
分析 根据平行线分线段成比例得到$\frac{AE}{DE}=\frac{AG}{CG}$，$\frac{CG}{AG}=\frac{CF}{BF}$，根据已知条件得到$\frac{AG}{CG}$=2，求得$\frac{CF}{BF}$=$\frac{1}{2}$，即可得到结论．
解答 解：∵DC∥EF∥AB，
∴$\frac{AE}{DE}=\frac{AG}{CG}$，$\frac{CG}{AG}=\frac{CF}{BF}$，
∵AE=2ED，
∴$\frac{AG}{CG}$=2，
$\frac{（\;\;\;\;）}{（\;\;\;\;）}$∴$\frac{CF}{BF}$=$\frac{1}{2}$，
∵CF=2cm，
∴BF=4cm，
∴BC=BF+CF=6cm．
点评 本题考查了平行线分线段成比例定理．熟练掌握平行线分线段成比例定理是解题的关键．
练习册系列答案
应用题天天练四川大学出版社系列答案
相关题目
18．在实数范围内因式分解2x2-3xy-y2，下列四个答案中正确的是（ ）
| A． | （x-$\frac{3+\sqrt{17}}{4}$y）（x-$\frac{3-\sqrt{17}}{4}$y） | B． | （x+$\frac{3+\sqrt{17}}{4}$y）（x+$\frac{3-\sqrt{17}}{4}$y） | ||
| C． | 2（x-$\frac{3+\sqrt{17}}{4}$y）（x-$\frac{3-\sqrt{17}}{4}$y） | D． | 2（x+$\frac{3+\sqrt{17}}{4}$y）（x+$\frac{3-\sqrt{17}}{4}$y） |
（1）先化简，再求值（2x+3）（2x-3）-4x（x-1）+（x+2）2，其中x=3．
如图，四边形ABCD的对角线AC和BD相交于点E，如果△CDE的面积为3，△BCE的面积为4，△AED的面积为6，那么△ABE的面积为8．
如图，已知∠ACD=120°，∠B=40°，则∠A的度数为80度．