题目内容
6.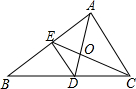 如图,在△ABC中,D、E分别为边BC、AB的中点,AD、CE相交于O,AB=8,BC=10,AC=6,求OD=$\frac{5}{3}$.
如图,在△ABC中,D、E分别为边BC、AB的中点,AD、CE相交于O,AB=8,BC=10,AC=6,求OD=$\frac{5}{3}$.
分析 根据勾股定理的逆定理得出∠BAC=90°,根据直角三角形斜边上中线性质求出AD,根据三角形中位线定理求出DE=$\frac{1}{2}$AC,DE∥AC,推出△DOE∽△AOC,得出比例式,即可求出答案.
解答 解:∵AB=8,BC=10,AC=6,
∴AB2+AC2=BC2,
∴∠BAC=90°,
∵D为BC的中点,
∴AD=$\frac{1}{2}$BC=$\frac{1}{2}$×10=5,
∵D、E分别为BC和AB的中点,
∴DE=$\frac{1}{2}$AC,DE∥AC,
∴△DOE∽△AOC,
∴$\frac{DO}{AO}$=$\frac{DE}{AC}$=$\frac{1}{2}$,
∴DO=$\frac{1}{3}$AD=$\frac{5}{3}$.
故答案为:$\frac{5}{3}$.
点评 本题考查了勾股定理的逆定理,直角三角形斜边上中线性质,三角形中位线定理,相似三角形的性质和判定的应用,能综合运用知识点进行推理是解此题的关键.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
1.下列各数中,无理数的是( )
| A. | 3 | B. | $\frac{22}{7}$ | C. | $\root{3}{8}$ | D. | $\sqrt{8}$ |
15.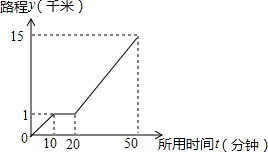 万州第四届山地自行车邀请赛在万州江南新区举行.当天,小强和同学明相约前往视看,小强从家出发先步行到小明家楼下的公交车站,等小了一会儿小明后两人一起乘公共汽车到达比赛地点,图中的折线表示小强离开家的路程y(千米)和所用时间x(分钟)之间的函数关系,则下列说法错误的是( )
万州第四届山地自行车邀请赛在万州江南新区举行.当天,小强和同学明相约前往视看,小强从家出发先步行到小明家楼下的公交车站,等小了一会儿小明后两人一起乘公共汽车到达比赛地点,图中的折线表示小强离开家的路程y(千米)和所用时间x(分钟)之间的函数关系,则下列说法错误的是( )
 万州第四届山地自行车邀请赛在万州江南新区举行.当天,小强和同学明相约前往视看,小强从家出发先步行到小明家楼下的公交车站,等小了一会儿小明后两人一起乘公共汽车到达比赛地点,图中的折线表示小强离开家的路程y(千米)和所用时间x(分钟)之间的函数关系,则下列说法错误的是( )
万州第四届山地自行车邀请赛在万州江南新区举行.当天,小强和同学明相约前往视看,小强从家出发先步行到小明家楼下的公交车站,等小了一会儿小明后两人一起乘公共汽车到达比赛地点,图中的折线表示小强离开家的路程y(千米)和所用时间x(分钟)之间的函数关系,则下列说法错误的是( )| A. | 小强家与小明家的路程为1千米 | |
| B. | 小强在小明家楼下的公共汽车站等10分钟 | |
| C. | 该公共汽车的平均速度为30 千米/小时 | |
| D. | 他们乘公共汽车用了30分钟 |
 (1)先化简,再求值(2x+3)(2x-3)-4x(x-1)+(x+2)2,其中x=3.
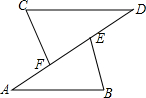
(1)先化简,再求值(2x+3)(2x-3)-4x(x-1)+(x+2)2,其中x=3. 如图,一次函数y=$\frac{2}{3}$x-2的图象分别与x轴.y轴交于点A.B,以线段AB为边在第四象限内作等腰Rt△ABC,∠BAC=90°,求过B、C两点直线的解析式.
如图,一次函数y=$\frac{2}{3}$x-2的图象分别与x轴.y轴交于点A.B,以线段AB为边在第四象限内作等腰Rt△ABC,∠BAC=90°,求过B、C两点直线的解析式.