题目内容
15. 如图,菱形ABCD,∠D=120°,E为菱形内一点,连结EC、EB.再将EB绕着点B逆时针旋转120°到FB,连结FA、EF,且EF交AB于点G.
如图,菱形ABCD,∠D=120°,E为菱形内一点,连结EC、EB.再将EB绕着点B逆时针旋转120°到FB,连结FA、EF,且EF交AB于点G.(1)求证:AF=CE;
(2)若∠EBC=45°,求∠AGE的大小.
分析 (1)先根据菱形的性质得出∠ABC=120°,AB=CB,再由图形旋转的性质得出EB=FB,根据SAS定理得出△AFB≌△CEB,由全等三角形的性质即可得出结论;
(2)先求出∠ABE的度数,再由等腰三角形的性质求出∠GEB的度数,再由∠AGE=∠ABE+∠GEB即可得出结论.
解答 解:(1)∵四边形ABCD是菱形,∠D=120°,
∴∠ABC=120°,AB=CB.
又∵EB绕着点B逆时针旋转120°到FB,
∴EB=FB,
∴∠FBA+∠ABE=∠ABE+∠EBC=120°,
∴∠FBA=∠EBC,
在△AFB与△CEB中,
∵$\left\{\begin{array}{l}EB=FB\\∠EBC=∠FBA\\ BC=AB\end{array}\right.$,
∴△AFB≌△CEB(SAS),
∴AF=CE;
(2)∵∠ABC=120°,∠EBC=45°,
∴∠ABE=75°.
又∵∠EBF=120°,EB=FB,
∴∠GEB=$\frac{180°-120°}{2}$=30°,
∴∠AGE=∠ABE+∠GEB=75°+30°=105°.
点评 本题考查的是旋转的性质,熟知图形旋转后所得图形与原图形全等是解答此题的关键.

练习册系列答案
相关题目
7.|-125|的立方根为( )
| A. | -5 | B. | 5 | C. | 25 | D. | ±5 |
5.若a>b,则下列式子正确的是( )
| A. | -3a>-3b | B. | 3a-1>3b-1 | C. | 3-a>3-b | D. | $\frac{1}{3}$a<$\frac{1}{3}$b |

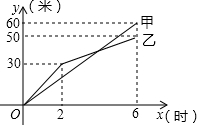 某市创建文明城区的活动中,有两段长度相等的彩色道转铺设任务,分别交给甲、乙两个施工队同时进行施工,如图是反映所铺设彩色道转的长度y(米)与施工时间x(时)之间关系的部分图象,请解答下列问题:
某市创建文明城区的活动中,有两段长度相等的彩色道转铺设任务,分别交给甲、乙两个施工队同时进行施工,如图是反映所铺设彩色道转的长度y(米)与施工时间x(时)之间关系的部分图象,请解答下列问题: 如图,直线a∥b,若∠1=60°,则∠2=60度.
如图,直线a∥b,若∠1=60°,则∠2=60度.