题目内容
16.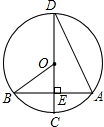 如图,已知⊙O的半径OB为3,且CD⊥AB,∠D=15°.则OE的长为( )
如图,已知⊙O的半径OB为3,且CD⊥AB,∠D=15°.则OE的长为( )| A. | $\frac{3}{2}\sqrt{3}$ | B. | $3\sqrt{3}$ | C. | $\frac{3}{2}$ | D. | 3 |
分析 连接OA,先根据圆O的直径为6求出OA的长,再由CD⊥AB得出∠AEO=90°,由圆周角定理求出∠AOE的度数,根据直角三角形的性质即可得出结论.
解答 解:连接OA,
∵圆O的直径为6,
∴OA=3.
∵CD⊥AB,
∴∠AEO=90°.
∵∠D=15°,
∴∠AOE=30°,
∴OE=OA•cos30°=3×$\frac{\sqrt{3}}{2}$=$\frac{3\sqrt{3}}{2}$.
故选A.
点评 本题考查的是垂径定理,熟知平分弦的直径平分这条弦,并且平分弦所对的两条弧是解答此题的关键.

练习册系列答案
相关题目
19.如果不等式组$\left\{\begin{array}{l}{-1<x≤3}\\{x>m}\end{array}\right.$ 有解,那么m的取值范围是( )
| A. | m≤3 | B. | m<3 | C. | m<-1 | D. | -1<m<3 |
11.某私家车每次加油都把油箱加满,如表记录了该车相邻两次加油时的情况
注:“累计里程”指汽车从出厂开始累计行驶的路程,在这段时间内,该车每100千米平均耗油量为( )
| 加油时间 | 加油量(升) | 加油时的累计里程(千米) |
| 2016年2月8日 | 12 | 35000 |
| 2016年2月12日 | 48 | 35600 |
| A. | 6升 | B. | 10升 | C. | 8升 | D. | 12升 |
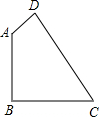 如图,四边形ABCD中,AB=BC=2,AD=1,CD=$\sqrt{7}$,∠B=90°,求四边形ABCD的面积.
如图,四边形ABCD中,AB=BC=2,AD=1,CD=$\sqrt{7}$,∠B=90°,求四边形ABCD的面积.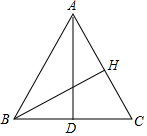 如图,AD是△ABC的中线,AD=12,AB=13,BC=10,
如图,AD是△ABC的中线,AD=12,AB=13,BC=10,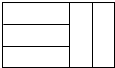 五个完全相同的小长方形拼成如图所示的大长方形,大长方形的周长是16cm,则小长方形的面积是3 cm 2.
五个完全相同的小长方形拼成如图所示的大长方形,大长方形的周长是16cm,则小长方形的面积是3 cm 2.