题目内容
17.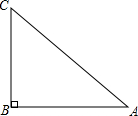 在△ABC中,如图所示,∠B=90°,AC=5$\sqrt{2}$,BC=5,解这个直角三角形.
在△ABC中,如图所示,∠B=90°,AC=5$\sqrt{2}$,BC=5,解这个直角三角形.
分析 根据∠B=90°,AC=5$\sqrt{2}$,BC=5,由勾股定理可得AB的长度,根据sinA=$\frac{BC}{AC}$,可以得到∠A的度数,从而得到∠C的度数.
解答 解:∵在△ABC中,∠B=90°,AC=5$\sqrt{2}$,BC=5,
∴AB=$\sqrt{A{C}^{2}-B{C}^{2}}=\sqrt{(5\sqrt{2})^{2}-{5}^{2}}$=$\sqrt{25}=5$.
∵sinA=$\frac{BC}{AC}$,BC=5,AC=5$\sqrt{2}$,
∴sinA=$\frac{\sqrt{2}}{2}$.
∴∠A=45°.
∴∠C=90°-∠A=90°-45°=45°.
即:AB=5,∠A=45°,∠C=45°.
点评 本题考查解直角三角形,解题的关键是明确直角三角形中,角角关系、边边关系、边角关系.

练习册系列答案
相关题目
7. 已知图中的两个三角形全等,则∠1等于( )
已知图中的两个三角形全等,则∠1等于( )
 已知图中的两个三角形全等,则∠1等于( )
已知图中的两个三角形全等,则∠1等于( )| A. | 50° | B. | 58° | C. | 60° | D. | 72° |
 如图,B是线段AD上一动点,沿A→D→A以2cm/s的速度往返运动1次,C是线段BD的中点,AD=10cm,设点B运动时间为t秒(0≤t≤10).
如图,B是线段AD上一动点,沿A→D→A以2cm/s的速度往返运动1次,C是线段BD的中点,AD=10cm,设点B运动时间为t秒(0≤t≤10). 如图,等边三角形ABC中,BD是AC边上的中线,BD=BE,则∠EDA=15 度.
如图,等边三角形ABC中,BD是AC边上的中线,BD=BE,则∠EDA=15 度.