题目内容
12. 如图,等边三角形ABC中,BD是AC边上的中线,BD=BE,则∠EDA=15 度.
如图,等边三角形ABC中,BD是AC边上的中线,BD=BE,则∠EDA=15 度.
分析 根据等边三角形的性质得到∠ABD=$\frac{1}{2}∠$ABC=30°,∠ADB=90°,根据等腰三角形的性质得到∠BDE=∠BED=$\frac{180°-30°}{2}$=75°,于是得到结论.
解答 解:∵等边三角形ABC中,BD是AC边上的中线,
∴∠ABD=$\frac{1}{2}∠$ABC=30°,∠ADB=90°,
∵BD=BE,
∴∠BDE=∠BED=$\frac{180°-30°}{2}$=75°,
∴∠EDA=15°.
故答案为:15.
点评 本题考查了等边三角形的性质,等腰三角形的性质,熟练掌握等边三角形的性质是解题的关键.

练习册系列答案
 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案
相关题目
2.三角形两边长分别为3和6,第三边的长是方程x2-15x+50=0的两根,则该三角形的周长为( )
| A. | 14 | B. | 15 | C. | 19 | D. | 14或19 |
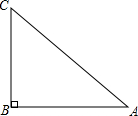 在△ABC中,如图所示,∠B=90°,AC=5$\sqrt{2}$,BC=5,解这个直角三角形.
在△ABC中,如图所示,∠B=90°,AC=5$\sqrt{2}$,BC=5,解这个直角三角形.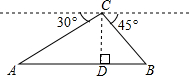 如图,从坡顶C处测得地面A、B两点的俯角分别为30°、45°,如果此时C出的高度CD为150米,且点A、D、B在同一直线上,则AB两点间距离是(150$\sqrt{3}$+150)米.
如图,从坡顶C处测得地面A、B两点的俯角分别为30°、45°,如果此时C出的高度CD为150米,且点A、D、B在同一直线上,则AB两点间距离是(150$\sqrt{3}$+150)米.