题目内容
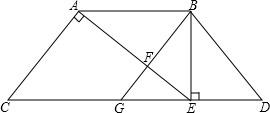 如图,在等腰梯形ABDC中,AC=BD,AB∥CD,过点B作BE⊥CD,垂足为E,连接AE,且∠CAE=90°,若∠ABF=∠D,
如图,在等腰梯形ABDC中,AC=BD,AB∥CD,过点B作BE⊥CD,垂足为E,连接AE,且∠CAE=90°,若∠ABF=∠D,求证:
(1)△ABF∽△ECA;
(2)若延长BF交CD与点G,判断四边形ABGC的形状并说明理由.
(3)当AB=4,BE=3时,求梯形ABDC的面积.
考点:相似三角形的判定与性质,等腰梯形的性质
专题:
分析:(1)证明∠BAF=∠AEC;证明∠ABF=∠C,即可解决问题.
(2)证明∠BGD=∠C,进而得到AC∥BG,即可解决问题.
(3)根据题意,求出AE、DE的长,即可解决问题.
(2)证明∠BGD=∠C,进而得到AC∥BG,即可解决问题.
(3)根据题意,求出AE、DE的长,即可解决问题.
解答: 解:(1)如图,∵AB∥CD,
解:(1)如图,∵AB∥CD,
∴∠BAF=∠AEC;
∵四边形ABCD是等腰梯形,
∴∠C=∠D;而∠ABF=∠D,
∴∠ABF=∠C,
∴△ABF∽△ECA.
(2)∵AB∥CD,
∴∠ABF=∠BGD;而∠ABF=∠D,∠C=∠D,
∴∠BGD=∠C,
∴AC∥BG;而AB∥CG,
∴四边形ABGC是平行四边形.
(3)∵AB∥CD,BE⊥CD,
∴AB⊥BE;而AB=4,BE=3,
由勾股定理得:AE=5.
∵∠BAE=∠AEC,∠ABE=∠CAE,
∴△ABE∽△EAC,
∴AB:AE=BE:AC=AE:CE,
即4:5=3:AC=5:CE,
∴AC=
,CE=
;
∴BD=AC=
;由勾股定理得:
DE2=BD2-BE2,
∴DE=
,CD=
+
=
,
∴梯形ABDC的面积=
(4+
)×3
=
.
 解:(1)如图,∵AB∥CD,
解:(1)如图,∵AB∥CD,∴∠BAF=∠AEC;
∵四边形ABCD是等腰梯形,
∴∠C=∠D;而∠ABF=∠D,
∴∠ABF=∠C,
∴△ABF∽△ECA.
(2)∵AB∥CD,
∴∠ABF=∠BGD;而∠ABF=∠D,∠C=∠D,
∴∠BGD=∠C,
∴AC∥BG;而AB∥CG,
∴四边形ABGC是平行四边形.
(3)∵AB∥CD,BE⊥CD,
∴AB⊥BE;而AB=4,BE=3,
由勾股定理得:AE=5.
∵∠BAE=∠AEC,∠ABE=∠CAE,
∴△ABE∽△EAC,
∴AB:AE=BE:AC=AE:CE,
即4:5=3:AC=5:CE,
∴AC=
| 15 |
| 4 |
| 25 |
| 4 |
∴BD=AC=
| 15 |
| 4 |
DE2=BD2-BE2,
∴DE=
| 9 |
| 4 |
| 25 |
| 4 |
| 9 |
| 4 |
| 17 |
| 2 |
∴梯形ABDC的面积=
| 1 |
| 2 |
| 17 |
| 2 |
=
| 75 |
| 4 |
点评:该题主要考查了梯形的性质、相似三角形的判定及其性质等几何知识点的应用问题;解题的关键是数形结合,准确找出命题图形中隐含的等量关系;灵活解题.

练习册系列答案
相关题目
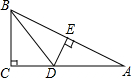 如图,在Rt△ABC中,∠C=90°,AB的垂直平分线交AC于点D,交AB于点E.若BC=2,AC=4,则BD=( )
如图,在Rt△ABC中,∠C=90°,AB的垂直平分线交AC于点D,交AB于点E.若BC=2,AC=4,则BD=( )A、
| ||
| B、2 | ||
C、
| ||
| D、3 |
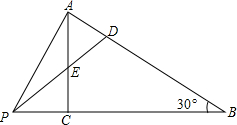 如图,在Rt△ABC中,∠ACB=90°.D、E分别是边AB、AC上的点,且AD=AE=1,连接DE并延长,与线段BC的延长线交于点P.
如图,在Rt△ABC中,∠ACB=90°.D、E分别是边AB、AC上的点,且AD=AE=1,连接DE并延长,与线段BC的延长线交于点P.
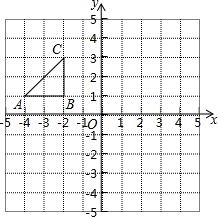 在平面直角坐标系中,△ABC的顶点坐标A(-4,1),B(-2,1),C(-2,3)
在平面直角坐标系中,△ABC的顶点坐标A(-4,1),B(-2,1),C(-2,3)