题目内容
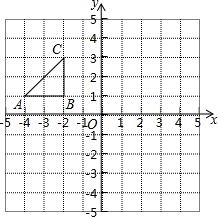 在平面直角坐标系中,△ABC的顶点坐标A(-4,1),B(-2,1),C(-2,3)
在平面直角坐标系中,△ABC的顶点坐标A(-4,1),B(-2,1),C(-2,3)(1)作△ABC关于y轴的对称图形△A1B1C1;
(2)将△ABC向下平移4个单位长度,作出平移后的△A2B2C2;
(3)求四边形AA2B2C的面积.
考点:作图-轴对称变换,作图-平移变换
专题:
分析:(1)分别作出点A、B、C关于y轴的对称的点,然后顺次连接;
(2)分别作出点A、B、C向下平移4个单位长度后的点,然后顺次连接;
(3)根据梯形的面积公式求出四边形AA2B2C的面积即可.
(2)分别作出点A、B、C向下平移4个单位长度后的点,然后顺次连接;
(3)根据梯形的面积公式求出四边形AA2B2C的面积即可.
解答:解:(1)(2)所作图形如图所示:
 ;
;
(3)四边形AA2B2C的面积为:
(4+6)×2=10.
即四边形AA2B2C的面积为10.
 ;
;(3)四边形AA2B2C的面积为:
| 1 |
| 2 |
即四边形AA2B2C的面积为10.
点评:本题考查了根据平移变换和轴对称变换作图,解答本题的关键是根据网格结构作出对应点,然后顺次连接.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,把一张长方形纸片ABCD沿EF折叠,点C、D分别落在点C′、D′的位置上,EC交AD于G,已知∠EFG=56°,那么∠BEG=
如图,把一张长方形纸片ABCD沿EF折叠,点C、D分别落在点C′、D′的位置上,EC交AD于G,已知∠EFG=56°,那么∠BEG= 正方体的六个面分别标有1,2,3,4,5,6六个数字,如图是其三种不同的放置方式,与数字“6”相对的面上的数字是( )
正方体的六个面分别标有1,2,3,4,5,6六个数字,如图是其三种不同的放置方式,与数字“6”相对的面上的数字是( )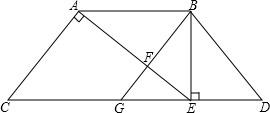 如图,在等腰梯形ABDC中,AC=BD,AB∥CD,过点B作BE⊥CD,垂足为E,连接AE,且∠CAE=90°,若∠ABF=∠D,
如图,在等腰梯形ABDC中,AC=BD,AB∥CD,过点B作BE⊥CD,垂足为E,连接AE,且∠CAE=90°,若∠ABF=∠D, 教练对小明推铅球的录像进行技术分析,发现铅球行进高度y(m)与水平距离x(m)之间的关系为y=-
教练对小明推铅球的录像进行技术分析,发现铅球行进高度y(m)与水平距离x(m)之间的关系为y=-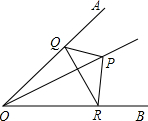 如图,∠AOB=45°,角内有一点P,PO=10,在角两边上有两点Q、R(均不同于点O),则△PQR的周长最小值是
如图,∠AOB=45°,角内有一点P,PO=10,在角两边上有两点Q、R(均不同于点O),则△PQR的周长最小值是