题目内容
14.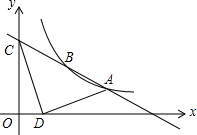 如图,已知反比例函数y=$\frac{k}{x}$与一次函数y=ax+b的图象交于A(4,1)、B(2,2)两点,一次函数的图象与y轴的交点为C.
如图,已知反比例函数y=$\frac{k}{x}$与一次函数y=ax+b的图象交于A(4,1)、B(2,2)两点,一次函数的图象与y轴的交点为C.(1)求反比例函数的解析式;
(2)直接写出在第一象限内一次函数大于反比例函数的值的x的取值范围;
(3)若点D的坐标为(1,0),求△ACD的面积.
分析 (1)把点A或B的坐标代入反比例函数解析式,求k的值,即可求出函数解析式;
(2)由图象观察可直接得出;
(3)利用一次函数图象上点的坐标特征求得点C的坐标;然后由S△ACD=S梯形AEOC-S△COD-S△DEA进行解答.
解答 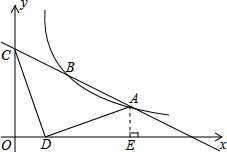 解:(1)∵点A(4,1)在反比例函数y=$\frac{k}{x}$上,
解:(1)∵点A(4,1)在反比例函数y=$\frac{k}{x}$上,
∴m=xy=4×1=4,
∴y=$\frac{4}{x}$;
(2)∵A(4,1)、B(2,2),
∴有图象可以看出,一次函数大于反比例函数的值的x的取值范围:2<x<4;
(3)∵把A(4,1),B(2,2)代入y=kx+b
∴$\left\{\begin{array}{l}{1=4k+b}\\{2=2k+b}\end{array}\right.$
解得$\left\{\begin{array}{l}{k=-\frac{1}{2}}\\{b=3}\end{array}\right.$,
∴一次函数的解析式为y=-$\frac{1}{2}$x+3,
∵点C在直线y=y=-$\frac{1}{2}$x+3上,
∴当x=0时,y=3,
∴C(0,3)
过A作AE⊥x轴于E.
∴S△ACD=S梯形AEOC-S△COD-S△DEA=$\frac{(1+3)×4}{2}$-$\frac{1}{2}$×1×3-$\frac{1}{2}$×1×3=5.
点评 本题考查了待定系数法求函数解析式,反比例函数与一次函数的交点问题,解题时,注意“数形结合”数学思想的应用.

练习册系列答案
相关题目
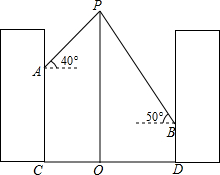 如图,某学校的两栋教学楼正中间有一个旗杆OP,旗杆底端O与两楼底部C、D在同一直线上,且OC=OD=10米,小明在图中左侧搂上点C的正上方A处测得旗杆顶端P的仰角为40°,小刚在图中右侧楼上点D的正上方B处测得旗杆顶端P的仰角为50°,侧得AC=8米,试求旗秆OP的长度和BD的长(参考数据:tan40°≈0.84,tan50°≈1.19,结果精确到0.1米)
如图,某学校的两栋教学楼正中间有一个旗杆OP,旗杆底端O与两楼底部C、D在同一直线上,且OC=OD=10米,小明在图中左侧搂上点C的正上方A处测得旗杆顶端P的仰角为40°,小刚在图中右侧楼上点D的正上方B处测得旗杆顶端P的仰角为50°,侧得AC=8米,试求旗秆OP的长度和BD的长(参考数据:tan40°≈0.84,tan50°≈1.19,结果精确到0.1米)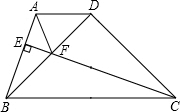 如图,在梯形ABCD中,AD∥BC,CE⊥AB于E,△BDC为等腰直角三角形,∠BDC=90°,BD=CD,CE与BD交于F,连接AF,求证:CF=AB+AF.
如图,在梯形ABCD中,AD∥BC,CE⊥AB于E,△BDC为等腰直角三角形,∠BDC=90°,BD=CD,CE与BD交于F,连接AF,求证:CF=AB+AF.
 如图,E,F是?ABCD对角线AC上的两点,且AE=CF.求证:∠1=∠2.
如图,E,F是?ABCD对角线AC上的两点,且AE=CF.求证:∠1=∠2.