题目内容
9. 如图,PA⊥PB,PD⊥AD,垂足分别为A,D,PA=PD,求证:AC=DC.
如图,PA⊥PB,PD⊥AD,垂足分别为A,D,PA=PD,求证:AC=DC.
分析 证明Rt△PAB≌Rt△PDB,得到∠ABP=∠DBP,AB=DB,再证明△ABC≌△DBC,得到AC=DC.
解答 解:∵PA⊥PB,PD⊥BD,
∴∠PAB=∠PDB=90°,
在Rt△PAB和Rt△PDB中,
$\left\{\begin{array}{l}{PA=PD}\\{PB=PB}\end{array}\right.$,
∴Rt△PAB≌Rt△PDB,
∴∠ABP=∠DBP,AB=DB,
在△ABC和△DBC中,
$\left\{\begin{array}{l}{AB=DB}\\{∠ABP=∠DBP}\\{BC=BC}\end{array}\right.$,
∴△ABC≌△DBC,
∴AC=DC.
点评 本题考查了全等三角形的性质与判定,解决本题的关键是证明Rt△PAB≌Rt△PDB和△ABC≌△DBC.

练习册系列答案
相关题目
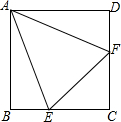 如图所示,在正方形ABCD中,∠EAF=45°,∠EAF绕点A顺时针旋转,它的两边分别交CB,DC(或它们的延长线)于点E、F.当∠EAF绕点A旋转到BE=DF时,连接EF.小明发现BE+DF=EF,你同意他的看法吗?说明理由.
如图所示,在正方形ABCD中,∠EAF=45°,∠EAF绕点A顺时针旋转,它的两边分别交CB,DC(或它们的延长线)于点E、F.当∠EAF绕点A旋转到BE=DF时,连接EF.小明发现BE+DF=EF,你同意他的看法吗?说明理由.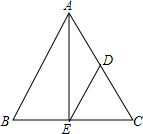 如图,△ABC中,AB=AC,点D,E分别在AC,BC上,且DA=DE,DE∥AB,求证:E是BC的中点.
如图,△ABC中,AB=AC,点D,E分别在AC,BC上,且DA=DE,DE∥AB,求证:E是BC的中点. 如图,在∠AOB内部一找P,使点P到OA和BO的距离相等,且到点O的距离等于2.5厘米,请你在图中找出这个点.
如图,在∠AOB内部一找P,使点P到OA和BO的距离相等,且到点O的距离等于2.5厘米,请你在图中找出这个点. 看图填空,如图:
看图填空,如图: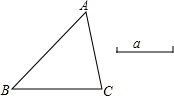 已知△ABC和线段a,且a>$\frac{1}{2}$BC,用直尺和圆规求作⊙O.使⊙O经过B,C两点,且半径为a,并说出可以作出几个圆(要求写出作法).
已知△ABC和线段a,且a>$\frac{1}{2}$BC,用直尺和圆规求作⊙O.使⊙O经过B,C两点,且半径为a,并说出可以作出几个圆(要求写出作法).