题目内容
12.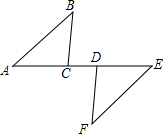 如图,△ABC≌△EFD,∠A与∠E是对应角.
如图,△ABC≌△EFD,∠A与∠E是对应角.(1)填空:那么,∠BCA与∠FDE是对应角,AC与ED是对应边;
(2)若∠A=45°,∠B=42°,AD=3cm,求∠EDF的度数和EC的长.
分析 (1)根据题意得出∠BCA与∠FDE是对应角,AC与ED是对应边;
(2)由全等三角形的性质得出∠E=∠A=45°,∠F=∠B=42°,ED=AC,由三角形内角和定理得出∠EDF=180°-∠E-∠F,EC=AD,即可得出结果.
解答 解:(1)∵△ABC≌△EFD,∠A与∠E是对应角.
∴∠BCA与∠FDE是对应角,AC与ED是对应边;
故答案为:∠FDE,ED;
(2)∵△ABC≌△EFD,
∴∠E=∠A=45°,∠F=∠B=42°,ED=AC,
∴∠EDF=180°-∠E-∠F=180°-45°-42°=93°,
EC=AD=3cm.
点评 本题考查了全等三角形的性质、三角形内角和定理;熟练掌握全等三角形的性质,并能进行推理计算是解决问题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
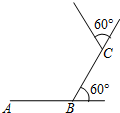 如图,小东在操场的中心位置,从点A出发,每走6m向左转60°,
如图,小东在操场的中心位置,从点A出发,每走6m向左转60°,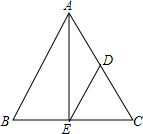 如图,△ABC中,AB=AC,点D,E分别在AC,BC上,且DA=DE,DE∥AB,求证:E是BC的中点.
如图,△ABC中,AB=AC,点D,E分别在AC,BC上,且DA=DE,DE∥AB,求证:E是BC的中点. 如图,在∠AOB内部一找P,使点P到OA和BO的距离相等,且到点O的距离等于2.5厘米,请你在图中找出这个点.
如图,在∠AOB内部一找P,使点P到OA和BO的距离相等,且到点O的距离等于2.5厘米,请你在图中找出这个点. 已知:如图,在四边形ABCD中,AD∥BC,点E是CD边的中点,且AB=BC+AD,求证:BE⊥AE.
已知:如图,在四边形ABCD中,AD∥BC,点E是CD边的中点,且AB=BC+AD,求证:BE⊥AE.