题目内容
14.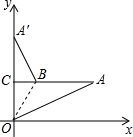 如图,Rt△AOC在平面直角坐标系中,OC在y轴上.OC=2,OA=5.将△AOC沿OB翻折使点A恰好落在y轴上的点A′的位置,则AB=$\frac{5\sqrt{21}}{7}$.
如图,Rt△AOC在平面直角坐标系中,OC在y轴上.OC=2,OA=5.将△AOC沿OB翻折使点A恰好落在y轴上的点A′的位置,则AB=$\frac{5\sqrt{21}}{7}$.
分析 由折叠的性质得:A′B=AB,OA′=OA=5,则A′C=3,由勾股定理求得AC设A′B=AB=x,则BC=$\sqrt{21}$-x,在Rt△A′BC中,由勾股定理可求得结论.
解答 解:由折叠的性质得:A′B=AB,OA′=OA=5,
∴A′C=3,
∵AC=$\sqrt{O{A}^{2}-O{C}^{2}}$=$\sqrt{{5}^{2}-{2}^{2}}$=$\sqrt{21}$,
设A′B=AB=x,
则BC=$\sqrt{21}$-x,
在Rt△A′BC中,
${x}^{2}={3}^{2}+(\sqrt{21}-x)^{2}$,
解得:x=$\frac{5\sqrt{21}}{7}$,
故答案为:$\frac{5\sqrt{21}}{7}$.
点评 本题主要考查了折叠问题,勾股定理得性质,能综合应用勾股定理和方程解决问题是解决此问题的关键.

练习册系列答案
相关题目
9.下列方程中,是关于x的一元二次方程是( )
| A. | x2+2x=x2-1 | B. | $\frac{1}{x}$-1=2x2=0 | C. | ax2+bx+c=0 | D. | (x+1)2=2(x+1) |
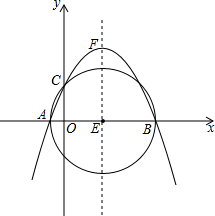 如图坐标系中,点E坐标(3,0),以E为圆心,5为半径作⊙E与x轴交于A,B两点,与y轴正半轴交于C点,抛物线y=ax2+bx+c经过A,B,C三点,顶点为F.
如图坐标系中,点E坐标(3,0),以E为圆心,5为半径作⊙E与x轴交于A,B两点,与y轴正半轴交于C点,抛物线y=ax2+bx+c经过A,B,C三点,顶点为F. 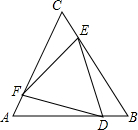 三边相等,三个角也相等的三角形叫做等边三角形,如图,△ABC和△DEF都是等边三角形,且D、E、F分别在AB、BC、CA边上.求证:AD=BE=CF.
三边相等,三个角也相等的三角形叫做等边三角形,如图,△ABC和△DEF都是等边三角形,且D、E、F分别在AB、BC、CA边上.求证:AD=BE=CF.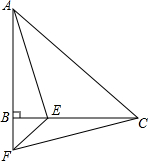 在△ABC中,AB=BC,∠ABC=90°,F为AB延长线上一点,点E,在BC上,BE=BF,连结AE,EF和CF,此时,若∠CAE=30°,那么∠EFC=30°.
在△ABC中,AB=BC,∠ABC=90°,F为AB延长线上一点,点E,在BC上,BE=BF,连结AE,EF和CF,此时,若∠CAE=30°,那么∠EFC=30°.