题目内容
7.从0,1,2,3,4,这五个数字中,随机抽取一个数,记为a,使得不等式组$\left\{\begin{array}{l}{2x-1<3}\\{x<a}\end{array}\right.$的解集是x<2,且使关于x的一元二次方程(a+1)x2+2$\sqrt{2}$x+$\frac{1}{2}$=0有两个实数根,则a的取值可能为2,3.分析 先根据不等式组$\left\{\begin{array}{l}{2x-1<3}\\{x<a}\end{array}\right.$的解集是x<2求出a的取值范围,再由关于x的一元二次方程(a+1)x2+2$\sqrt{2}$x+$\frac{1}{2}$=0有两个实数根得出a的取值范围,取其公共部分即可.
解答 解:∵不等式不等式组$\left\{\begin{array}{l}{2x-1<3}\\{x<a}\end{array}\right.$的解集是x<2,
∴a≥2.
∵关于x的一元二次方程(a+1)x2+2$\sqrt{2}$x+$\frac{1}{2}$=0有两个实数根,
∴$\left\{\begin{array}{l}a+1≠0\\△=8-2(a+1)>0\end{array}\right.$,解得a≤3,
∴a的取值可能为2.
故答案为:2,3.
点评 本题考查的是概率公式,根据题意得出a的取值范围是解答此题的关键.

练习册系列答案
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目
17.若a+b=7,ab=5,则(a-b)2=( )
| A. | 25 | B. | 29 | C. | 69 | D. | 75 |
 如图,若
如图,若 所在位置的坐标为(-1,-2),
所在位置的坐标为(-1,-2), 所在的位置的坐标为(2,-2),请用坐标表示出
所在的位置的坐标为(2,-2),请用坐标表示出 所在的位置(-3,2).
所在的位置(-3,2).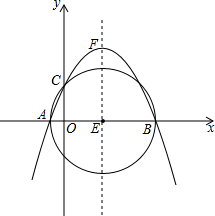 如图坐标系中,点E坐标(3,0),以E为圆心,5为半径作⊙E与x轴交于A,B两点,与y轴正半轴交于C点,抛物线y=ax2+bx+c经过A,B,C三点,顶点为F.
如图坐标系中,点E坐标(3,0),以E为圆心,5为半径作⊙E与x轴交于A,B两点,与y轴正半轴交于C点,抛物线y=ax2+bx+c经过A,B,C三点,顶点为F. 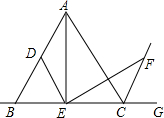 如图,△ABC是等边三角形,∠AEF=60°,ED∥AC交AB于点D,EF,交等边三角形外角平分线CF所在的直线与点F,当点E是BC的中点时,求证:AE=EF.
如图,△ABC是等边三角形,∠AEF=60°,ED∥AC交AB于点D,EF,交等边三角形外角平分线CF所在的直线与点F,当点E是BC的中点时,求证:AE=EF.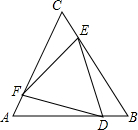 三边相等,三个角也相等的三角形叫做等边三角形,如图,△ABC和△DEF都是等边三角形,且D、E、F分别在AB、BC、CA边上.求证:AD=BE=CF.
三边相等,三个角也相等的三角形叫做等边三角形,如图,△ABC和△DEF都是等边三角形,且D、E、F分别在AB、BC、CA边上.求证:AD=BE=CF.