题目内容
抛物线y=
x2-x-4与x轴交于A、B两点,P为直线y=kx+4k(k>0)上的动点,若使△ABP为直角三角形的点P有且只有三个,则k= .
| 1 |
| 2 |
考点:抛物线与x轴的交点
专题:
分析:可先求得A、B的坐标,当使△ABP为直角三角形的点P有且只有三个时可知直线y=kx+4k与以AB为直径的圆相切,可求得k值.
解答: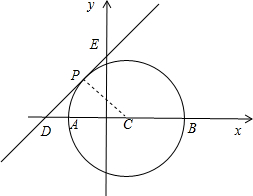 解:在抛物线y=
解:在抛物线y=
x2-x-4中令y=0,可得
x2-x-4=0,解得x=-2或x=4,
故A、B两点的坐标为(-2,0)和(4,0),
如图,以AB为直径画圆C,则当直线与圆相离时,满足条件的P点有两个,当直线与圆相交时,满足条件的P点有4个,
故使△ABP为直角三角形的点P有且只有三个时,直线与圆相切,
设切点为P,直线与x轴、y轴分别交与点D、E,连接CP,
在y=kx+4k中令y=0,可求得x=-4,
∴OD=4,且OC=1,
∴CD=5,在Rt△CDP中,PC=3,可求得PD=4,
又∵∠PDO=∠PDO,∠POD=∠DPC,
∴△EDO∽△CDP,
∴
=
,即
=
,
解得OE=5,即E点坐标为(0,4),
∴4k=4,
解得k=1.
故答案为:1.
 解:在抛物线y=
解:在抛物线y=| 1 |
| 2 |
| 1 |
| 2 |
故A、B两点的坐标为(-2,0)和(4,0),
如图,以AB为直径画圆C,则当直线与圆相离时,满足条件的P点有两个,当直线与圆相交时,满足条件的P点有4个,
故使△ABP为直角三角形的点P有且只有三个时,直线与圆相切,
设切点为P,直线与x轴、y轴分别交与点D、E,连接CP,
在y=kx+4k中令y=0,可求得x=-4,
∴OD=4,且OC=1,
∴CD=5,在Rt△CDP中,PC=3,可求得PD=4,
又∵∠PDO=∠PDO,∠POD=∠DPC,
∴△EDO∽△CDP,
∴
| OD |
| PD |
| PC |
| OE |
| 4 |
| 4 |
| 5 |
| OE |
解得OE=5,即E点坐标为(0,4),
∴4k=4,
解得k=1.
故答案为:1.
点评:本题主要考查函数与坐标轴的交点,确定出满足条件的直线所在的位置是解题的关键,注意相似三角形的判定和性质的利用.

练习册系列答案
相关题目
已知直角三角形的两条边长分别是3和5,那么这个三角形的第三条边的长为( )
| A、4 | ||
| B、16 | ||
C、
| ||
D、4或
|
 如图,在△ABC中,∠C=90°,AD平分∠CAB,交CB于点D,过点D作DE⊥AB于点E.
如图,在△ABC中,∠C=90°,AD平分∠CAB,交CB于点D,过点D作DE⊥AB于点E.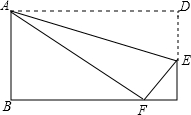 如图,矩形ABCD边上AD沿折痕AE折叠,使点D落在BC上的F处,已知AB=6,△ABF的面积是24,求FE的长.
如图,矩形ABCD边上AD沿折痕AE折叠,使点D落在BC上的F处,已知AB=6,△ABF的面积是24,求FE的长.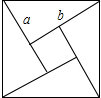 我国古代数学家赵给出的“弦图”是由四个全等的直角三角形与中间的一个小正方形拼成的一个大正方形(如图所示),如果大正方形的面积是5,小正方形的面积是1,直角三角形的两只角边长分别是a,b,那么(a+b)2的值是
我国古代数学家赵给出的“弦图”是由四个全等的直角三角形与中间的一个小正方形拼成的一个大正方形(如图所示),如果大正方形的面积是5,小正方形的面积是1,直角三角形的两只角边长分别是a,b,那么(a+b)2的值是