题目内容
 如图,在△ABC中,∠C=90°,AD平分∠CAB,交CB于点D,过点D作DE⊥AB于点E.
如图,在△ABC中,∠C=90°,AD平分∠CAB,交CB于点D,过点D作DE⊥AB于点E.(1)求证:△ACD≌△AED;
(2)若BC=8,BE=5,求△BDE的周长.
考点:全等三角形的判定与性质,勾股定理
专题:
分析:(1)易证CD=DE,即可证明RT△ACD≌RT△AED,即可解题;
(2)根据(1)中结论可得CD=DE,根据△BDE的周长=BD+DE+BE即可解题.
(2)根据(1)中结论可得CD=DE,根据△BDE的周长=BD+DE+BE即可解题.
解答:(1)证明:∵AD平分∠CAB,
∴CD=DE,
在RT△ACD和RT△AED中,
,
∴RT△ACD≌RT△AED(HL);
(2)∵RT△ACD≌RT△AED,
∴CD=DE,
∴△BDE的周长=BD+DE+BE=BD+CD+BE=13.
∴CD=DE,
在RT△ACD和RT△AED中,
|
∴RT△ACD≌RT△AED(HL);
(2)∵RT△ACD≌RT△AED,
∴CD=DE,
∴△BDE的周长=BD+DE+BE=BD+CD+BE=13.
点评:本题考查了全等三角形的判定,考查了全等三角形对应边相等的性质,本题中求证RT△ACD≌RT△AED是解题的关键.

练习册系列答案
相关题目
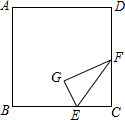 如图,把正方形ABCD的一个角向上折,EF为折痕,点C落在点G处,测得AD=30cm,BE=20cm,∠BEG=60°,求折痕EF的长.
如图,把正方形ABCD的一个角向上折,EF为折痕,点C落在点G处,测得AD=30cm,BE=20cm,∠BEG=60°,求折痕EF的长. 如图,在△ABC中,已知AB=4,AC=3,BC边上的高AD=2,则△ABC的外接圆半径等于
如图,在△ABC中,已知AB=4,AC=3,BC边上的高AD=2,则△ABC的外接圆半径等于 用直尺和圆规作图,保留作图痕迹,不写作法.
用直尺和圆规作图,保留作图痕迹,不写作法.