题目内容
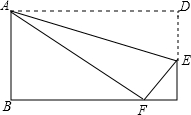如图，矩形ABCD边上AD沿折痕AE折叠，使点D落在BC上的F处，已知AB=6，△ABF的面积是24，求FE的长．考点：翻折变换（折叠问题）
专题：
分析：如图，根据题意结合图形，首先求出BF的长度，进而求出AF的长度；根据勾股定理列出关于线段EF的方程，即可解决问题．
解答：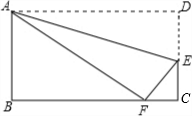
解：如图，∵四边形ABCD是矩形，
∴∠B=∠C=90°；DC=AB=6，BC=AD；
由题意得：EF=DE（设为λ），AF=AD，
∴BC=AF，EC=6-λ；
∵△ABF的面积是24，
∴
BF•AB=24，而AB=6，
∴BF=8；由勾股定理得：
AF2=AB2+BF2=100，
∴AF=10，BC=AF=10，FC=2；
由勾股定理得：λ2=（6-λ）2+22，
解得：λ=
，
即FE的长为
．
解：如图，∵四边形ABCD是矩形，∴∠B=∠C=90°；DC=AB=6，BC=AD；
由题意得：EF=DE（设为λ），AF=AD，
∴BC=AF，EC=6-λ；
∵△ABF的面积是24，
∴
| 1 |
| 2 |
∴BF=8；由勾股定理得：
AF2=AB2+BF2=100，
∴AF=10，BC=AF=10，FC=2；
由勾股定理得：λ2=（6-λ）2+22，
解得：λ=
| 10 |
| 3 |
即FE的长为
| 10 |
| 3 |
点评：该题主要考查了翻折变换及其应用问题；解题的关键是根据翻折变换的性质找出图形中隐含的等量关系，灵活运用勾股定理等几何知识来分析、探究、推理或解答．
练习册系列答案
相关题目
如图，在△ABC中，已知AB=4，AC=3，BC边上的高AD=2，则△ABC的外接圆半径等于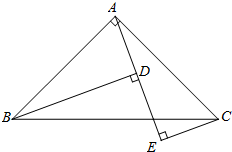
如图，已知△ABC中，∠BAC=90°，AB=AC，B、C在A、E的异侧，BD⊥AE于D，CE⊥AE于E．求证：
如图，在△ABC中，∠ACB=90°，∠A=20°，若将△ABC沿CD折叠，使点B落在AC边上的E处，则∠ADE的度数是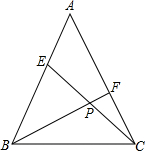
等腰△ABC中，AB=AC，E、F分别是AB、AC上的点，且BE=AF，连接CE、BF交于点P．若