题目内容
如果自然数n满足：对于n的每一个因数d，n÷d+d的值都是质数，那么就说n是一个“调皮数”，则50至200之间的所有“调皮数”之和是 ．
考点：质数与合数
专题：
分析：先根据“调皮数”的定义得到50至200之间的所有“调皮数”，再把它们相加即可求解．
解答：解：由“调皮数”的定义可知，
50至200之间的“调皮数”有58，70，78，82，130，190，
58+70+78+82+130+190=608．
故50至200之间的所有“调皮数”之和是608．
故答案为：608．
50至200之间的“调皮数”有58，70，78，82，130，190，
58+70+78+82+130+190=608．
故50至200之间的所有“调皮数”之和是608．
故答案为：608．
点评：考查了质数与合数，本题关键是理解“调皮数”的定义，找到50至200之间的所有“调皮数”．
练习册系列答案
相关题目
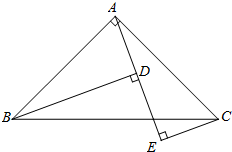如图，已知△ABC中，∠BAC=90°，AB=AC，B、C在A、E的异侧，BD⊥AE于D，CE⊥AE于E．求证：
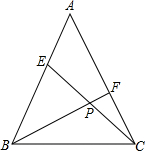等腰△ABC中，AB=AC，E、F分别是AB、AC上的点，且BE=AF，连接CE、BF交于点P．若
一个花坛的形状如图所示，它的两端是半径相等的半圆，求：已知在Rt△ABC中，∠C=90°，AC=3，BC=4，则tanA的值为（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
直线EF，CD相交于点O，OA⊥OB，且OC平分∠AOF，若∠AOF=140°，则∠BOD的度数为