Question

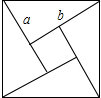我国古代数学家赵给出的“弦图”是由四个全等的直角三角形与中间的一个小正方形拼成的一个大正方形（如图所示），如果大正方形的面积是5，小正方形的面积是1，直角三角形的两只角边长分别是a，b，那么（a+b）²的值是

 

．

Answer 1

考点：勾股定理的证明

专题：

分析：根据正方形的面积公式以及勾股定理，结合图形进行分析发现：大正方形的面积即直角三角形斜边的平方5，也就是两条直角边的平方和是5，四个直角三角形的面积和是大正方形的面积减去小正方形的面积即2ab=5-1=4．根据完全平方公式即可求解．

解答：解：根据题意，结合勾股定理a²+b²=5，
四个三角形的面积=4×

1

2

ab=5-1，
∴2ab=4，
联立解得：（a+b）²=5+4=9．
故答案为：9．

点评：考查了勾股定理的证明，注意观察图形：发现各个图形的面积和a，b的关系．