题目内容
8.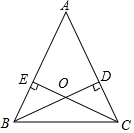 如图,已知在等腰三角形ABC中,AB=AC,BD⊥AC于点D,CE⊥AB于点E,CE与BD交于点O.
如图,已知在等腰三角形ABC中,AB=AC,BD⊥AC于点D,CE⊥AB于点E,CE与BD交于点O.(1)求证:△BCE≌△CBD;
(2)写出图中所有相等的线段.
分析 根据AB=AC,得出∠EBC=∠DCB,在△BCE和△CBD中,根据AAS即可证出△BCE≌△CBD.
解答 证明:(1)∵AB=AC,BD⊥AC,CE⊥AB,
∴∠ADB=∠AEC=90°,
在△ABD和△ACE中,
$\left\{\begin{array}{l}{∠ADB=∠AEC}\\{∠A=∠A}\\{AB=AC}\end{array}\right.$,
∴△ABD≌△ACE(AAS),
∴BD=CE;
∵AB=AC,
∴∠EBC=∠DCB,
在△BCE和△CBD中,
$\left\{\begin{array}{l}{∠EBC=∠DCB}\\{∠BEC=∠CDB}\\{BD=CE}\end{array}\right.$,
∴△BCE≌△CBD.
(2)相等的线段有:AB=AC,BE=CD,AE=AD,CE=BD,OB=OC,OE=OD.
点评 此题考查了全等三角形的判断与性质,根据AAS证出三角形全等是本题的关键,有两组角分别相等,且其中一组角所对的边相等,那么这两个三角形全等;全等三角形的对应边相等,对应角相等.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
19.小夏是一位善于观察、勤于动脑的学生.一天,他从2017年某个月日历表中随机框取了相邻的四个数(如图所示),分别用a,b,c,d表示.略加思考后,他写出了三个关系式:①a+c=b+d;②c-a=b-d;③ac-bd=7.其中正确的有( )
| 2017年 月 农历丙申(猴)年辛丑月 建国68年 | ||||||
| 日 | 一 | 二 | 三 | 四 | 五 | 六 |
| 1 初五 | 2 初六 | 3 立夏初七 | 4 初八 | |||
| a | d | |||||
| b | c | |||||
| A. | 3个 | B. | 2个 | C. | 1个 | D. | 0个 |
17. 如图,在等腰三角形ABC中,AB=AC,BD⊥AC,∠ABC=70°,则∠DBC等于( )
如图,在等腰三角形ABC中,AB=AC,BD⊥AC,∠ABC=70°,则∠DBC等于( )
 如图,在等腰三角形ABC中,AB=AC,BD⊥AC,∠ABC=70°,则∠DBC等于( )
如图,在等腰三角形ABC中,AB=AC,BD⊥AC,∠ABC=70°,则∠DBC等于( )| A. | 20° | B. | 30° | C. | 50° | D. | 70° |
 如图,平面直角坐标系中,已知直线y=x上一点P(1,1),C为y轴上一点,连接PC,线段PC绕点P顺时针旋转90°至线段PD,过点D作直线AB⊥x轴,垂足为B,直线AB与直线y=x交于点A,且BD=3AD,连接CD,直线CD与直线y=x交于点Q,则点Q的坐标为($\frac{32}{15}$,$\frac{32}{15}$).
如图,平面直角坐标系中,已知直线y=x上一点P(1,1),C为y轴上一点,连接PC,线段PC绕点P顺时针旋转90°至线段PD,过点D作直线AB⊥x轴,垂足为B,直线AB与直线y=x交于点A,且BD=3AD,连接CD,直线CD与直线y=x交于点Q,则点Q的坐标为($\frac{32}{15}$,$\frac{32}{15}$).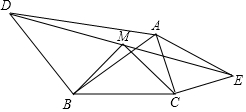 己知:如图,若△ABD和△ACE为等腰Rt△,AB=DB,AC=CE,M为DE中点,求证:△BMC为等腰Rt△.
己知:如图,若△ABD和△ACE为等腰Rt△,AB=DB,AC=CE,M为DE中点,求证:△BMC为等腰Rt△.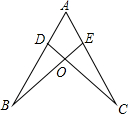 如图,点D,E分别在线段AB,AC上,CD与BE相交于O点、已知AB=AC,BD=CE,求证:∠B=∠C.
如图,点D,E分别在线段AB,AC上,CD与BE相交于O点、已知AB=AC,BD=CE,求证:∠B=∠C.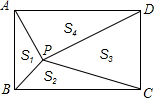 如图,点P是矩形ABCD内一点,连接PA、PB、PC、PD,已知AB=3,BC=4,设△PAB、△PBC、△PCD、△PDA的面积分别为S1、S2、S3、S4,以下判断:
如图,点P是矩形ABCD内一点,连接PA、PB、PC、PD,已知AB=3,BC=4,设△PAB、△PBC、△PCD、△PDA的面积分别为S1、S2、S3、S4,以下判断: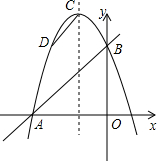 如图,一次函数y=x+3的图象与坐标轴分别交于A,B两点,二次函数y=ax2+bx-3a的图象经过点A,B.
如图,一次函数y=x+3的图象与坐标轴分别交于A,B两点,二次函数y=ax2+bx-3a的图象经过点A,B.