题目内容
平行四边行的两条对角线把它分成全等三角形的对数是( )
A. 2 B. 4 C. 6 D. 8
 B
【解析】【解析】
如图,?ABCD中,AC,DB分别分得△ABC≌△CDA,△ABD≌△CDB,
又对角线互相平分得到△AOD≌△COB,△AOB≌△COD,所以有4对.
故选B.
B
【解析】【解析】
如图,?ABCD中,AC,DB分别分得△ABC≌△CDA,△ABD≌△CDB,
又对角线互相平分得到△AOD≌△COB,△AOB≌△COD,所以有4对.
故选B.
练习册系列答案
相关题目
某工厂有一种产品现在的年产量是20万件,计划今后两年增加产量,如果每年都比上一年的产量增加x倍,那么两年后这种产品的产量y将随计划所定的x的值而确定,那么y与x之间的关系应表示为_____.
 y=20(x+1)2
【解析】∵某工厂一种产品的年产量是20件,每一年都比上一年的产品增加x倍,
∴一年后产品是:20(1+x),
∴两年后产品y与x的函数关系是:y=20(1+x)2.
故答案为:y=20(x+1)2.
y=20(x+1)2
【解析】∵某工厂一种产品的年产量是20件,每一年都比上一年的产品增加x倍,
∴一年后产品是:20(1+x),
∴两年后产品y与x的函数关系是:y=20(1+x)2.
故答案为:y=20(x+1)2. 任取不等式组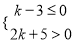 的一个整数解,则能使关于x的方程:2x+k=-1的解为非负数的可能性为____.
的一个整数解,则能使关于x的方程:2x+k=-1的解为非负数的可能性为____.
 【解析】解不等式k-3≤0可得k≤3,解不等式2k+5>0,可得k>-,所以可求得不等式组的解集为-<k≤3,所以k的整数解为-2、-1、0、1、2、3,分别代入方程2x+k=-1,可得x=、0、-、-1、-、-2,所以非负数解有了两个,其可能性为: .
故答案为: .
【解析】解不等式k-3≤0可得k≤3,解不等式2k+5>0,可得k>-,所以可求得不等式组的解集为-<k≤3,所以k的整数解为-2、-1、0、1、2、3,分别代入方程2x+k=-1,可得x=、0、-、-1、-、-2,所以非负数解有了两个,其可能性为: .
故答案为: . 和直线l距离为8 cm的直线有______条.
 2
【解析】【解析】
在同一平面上,和直线l距离为8cm的直线在直线L的两侧各有一条.故答案为:2.
2
【解析】【解析】
在同一平面上,和直线l距离为8cm的直线在直线L的两侧各有一条.故答案为:2. 下列不能作为判定四边形ABCD为平行四边形的条件的是( )
A. AB=CD,AD=BC B. AB CD
CD
C. AB=CD,AD∥BC D. AB∥CD,AD∥BC
 C
【解析】解:A.∵AB=CD,AD=BC,∴四边形ABCD的两组对边相等,可以判定四边形ABCD是平行四边形;故本选项不合题意;
B.∵AB∥CD,AB=CD,∴四边形ABCD的一组对边平行且相等,可以判定四边形ABCD是平行四边形;故本选项不合题意;
C.∵AB=CD,AD∥CD,无法判定四边形ABCD是平行四边形;故本选项合题意;
D.∵AB∥CD,AD∥BC,四边...
C
【解析】解:A.∵AB=CD,AD=BC,∴四边形ABCD的两组对边相等,可以判定四边形ABCD是平行四边形;故本选项不合题意;
B.∵AB∥CD,AB=CD,∴四边形ABCD的一组对边平行且相等,可以判定四边形ABCD是平行四边形;故本选项不合题意;
C.∵AB=CD,AD∥CD,无法判定四边形ABCD是平行四边形;故本选项合题意;
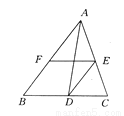
D.∵AB∥CD,AD∥BC,四边... 如图所示,AD为△ABC的一条角平分线,E,F分别在AC,AB上,DE∥AB,BF=AE.试说明EF=BD.
 答案见解析
【解析】试题分析:由角平分线的定义和平行线的性质可证明∠ADE=∠CAD,可得AE=DE,结合条件可证明四边形EFBD为平行四边形,可得EF=BD.
试题解析:证明:∵AD平分∠BAC,∴∠BAD=∠CAD.∵DE∥AB,∴∠BAD=∠ADE,∴∠CAD=∠ADE,∴AE=DE.又∵BF=AE,∴DE=BF.又∵DE∥AB,∴四边形EFBD是平行四边形,∴EF=BD.
...
答案见解析
【解析】试题分析:由角平分线的定义和平行线的性质可证明∠ADE=∠CAD,可得AE=DE,结合条件可证明四边形EFBD为平行四边形,可得EF=BD.
试题解析:证明:∵AD平分∠BAC,∴∠BAD=∠CAD.∵DE∥AB,∴∠BAD=∠ADE,∴∠CAD=∠ADE,∴AE=DE.又∵BF=AE,∴DE=BF.又∵DE∥AB,∴四边形EFBD是平行四边形,∴EF=BD.
... M是△ABC的AB边上的中点,连接CM并延长到D,使MD=CM,则AD与BC________,BD与AC________。
 平行且相等 平行且相等
【解析】【解析】
如图,∵M是△ABC的AB边上的中点,∴AM=MB.∵MD=CM,∴四边形ADBC是平行四边形,∴AD=CB,AD∥CB,BD=AC,BD∥AC.故答案为:平行且相等,平行且相等.
平行且相等 平行且相等
【解析】【解析】
如图,∵M是△ABC的AB边上的中点,∴AM=MB.∵MD=CM,∴四边形ADBC是平行四边形,∴AD=CB,AD∥CB,BD=AC,BD∥AC.故答案为:平行且相等,平行且相等. 已知实数a是不等于3的常数,解不等式组 ,并依据a的取值情况写出其解集.
,并依据a的取值情况写出其解集.
 当a>3时,不等式组的解集为x≤3;当a<3时,不等式组的解集为x<a.
【解析】试题分析:分别解两个不等式,然后根据不等式组的解集的确定法分情况讨论即可.
试题解析:【解析】
解①得:x≤3,解②得:x<a,
∵实数a是不等于3的常数,
∴当a>3时,不等式组的解集为x≤3;
当a<3时,不等式组的解集为x<a.
当a>3时,不等式组的解集为x≤3;当a<3时,不等式组的解集为x<a.
【解析】试题分析:分别解两个不等式,然后根据不等式组的解集的确定法分情况讨论即可.
试题解析:【解析】
解①得:x≤3,解②得:x<a,
∵实数a是不等于3的常数,
∴当a>3时,不等式组的解集为x≤3;
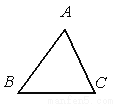
当a<3时,不等式组的解集为x<a. 如图,已知△ABC,AB<BC,用尺规作图的方法在BC上取一点P,使得PA+PC=BC,则下列选项正确的是( )
A. 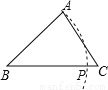 B.
B. 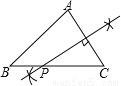 C.
C. 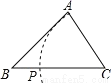 D.
D. 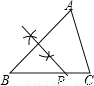
 D
【解析】试题分析:由PB+PC=BC和PA+PC=BC易得PA=PB,根据线段垂直平分线定理的逆定理可得点P在AB的垂直平分线上,于是可判断D选项正确.
故选D.
D
【解析】试题分析:由PB+PC=BC和PA+PC=BC易得PA=PB,根据线段垂直平分线定理的逆定理可得点P在AB的垂直平分线上,于是可判断D选项正确.
故选D. 
