题目内容
在等腰梯形ABCD中，AD∥BC，AE⊥BC于E，且AE=AD，BC＝3AE， 则∠BAD等于 （ ）
A. 120° B. 135° C. 130° D. 不能确定
B
【解析】【解析】
过点D作DF⊥BC于点F．
∵AE⊥BC，DF⊥BC，AD=AE，∴四边形AEFD为正方形，∴AD=EF．
∵AD=AE，BC=3AD，∴BE=AE=EF=FC，∴∠B=45°，∴∠BAD=135°．
故选B．
天天向上一本好卷系列答案
小学生10分钟应用题系列答案广东特产专卖店销售龙眼干，其进价为每斤40元，按每斤60元出售，平均每天可售出100斤，后来经调查发现，单价每降低2元，则平均每天的销售量增加20斤．每斤降价多少元，每天销售额最大？
20元
【解析】
试题分析：根据题意可以列出销售额与销售单价之间的关系式，然后整理为顶点式，即可解答本题．
【解析】
设每斤降价x元，销售额为y元，
y=（60﹣x）（100+）=﹣10（x﹣25）2+12250，
∴当x＜25时，y随x的增大而增大，
∵60﹣40=20，
∴0≤x≤20，
∴当x=20时，y取得最大值，
即每斤降价20元时... 抛物线y=﹣（x+2）2﹣3的顶点坐标是（ ）
A. （2，﹣3） B. （﹣2，3） C. （2，3） D. （﹣2，﹣3）
D
【解析】试题分析：∵抛物线y=﹣（x+2）2﹣3为抛物线解析式的顶点式，∴抛物线顶点坐标是（﹣2，﹣3）．故选D． 如图所示，在直角梯形ABCD中，AD∥BC，∠B＝90°，AD＝24 ㎝，BC＝26㎝，动点P从点A开始沿AD边以每秒1㎝的速度向D点运动，动点Q从点C开始沿CB边以每秒3㎝的速度向B运动，P，Q分别从A，C同时出发，当其中一点到达端点时，另一点也随之停止运动，设运动时间为t s．
（1）t为何值时，四边形PQCD为平行四边形?
（2）t为何值时，四边形PQCD为等腰梯形?
（3）t为何值时，四边形ABQP为矩形?
（1）t＝6时；（2）t＝7时；（3）t＝时.
【解析】试题分析：（1）要使四边形PQCD是平行四边形，则点在运动的过程中，只需PD=QC就满足题意；
（2）作DE⊥BC，PF⊥BC，垂足分别为E，F，要使四边形PQCD为等腰梯形，则QF＝CE；依此即可求解；
（3）要使四边形ABQP为矩形，则点在运动的过程中，只需AP=BQ就满足题意．
试题解析：【解析】
由已知得AP... 和直线l距离为8 cm的直线有______条.
2
【解析】【解析】
在同一平面上，和直线l距离为8cm的直线在直线L的两侧各有一条．故答案为：2． □ABCD的周长为36 cm，AB=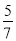
BC，则较长边的长为（ ）
A. 15 cm B. 7.5 cm C. 21 cm D. 10.5 cm
D
【解析】【解析】
∵?ABCD的周长=2（AB+BC）=36，∴AB+BC=18．∵AB=BC，∴BC=10.5．
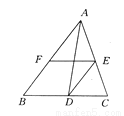
故选D． 如图所示，AD为△ABC的一条角平分线，E，F分别在AC，AB上，DE∥AB，BF＝AE．试说明EF＝BD．
答案见解析
【解析】试题分析：由角平分线的定义和平行线的性质可证明∠ADE=∠CAD，可得AE=DE，结合条件可证明四边形EFBD为平行四边形，可得EF=BD．
试题解析：证明：∵AD平分∠BAC，∴∠BAD=∠CAD．∵DE∥AB，∴∠BAD=∠ADE，∴∠CAD=∠ADE，∴AE=DE．又∵BF=AE，∴DE=BF．又∵DE∥AB，∴四边形EFBD是平行四边形，∴EF=BD．
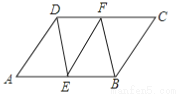
... 如图，平行四边形ABCD中，E，F分别为边AB，DC的中点，则图中共有平行四边形的个数是 （ ）
A. 3 B. 4 C. 5 D. 6
B
【解析】【解析】
∵四边形ABCD是平行四边形，∴AB∥CD，AB=CD．
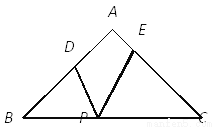
∵E，F分别AB，CD的中点，∴AE=EB=DF=FC，∴四边形AEFD是平行四边形，四边形EFCB是平行四边形，四边形BEDF是平行四边形，∴平行四边形的个数共有4个．故选B． 如图，在△ABC中，AB＝AC＝5，BC＝8，P是BC边上的动点，过点P作PD⊥AB于点D，PE⊥AC于点E，则PD+PE的长是（ ）
A. 4.8 B. 4.8或3.8 C. 3.8 D. 5
A
【解析】试题分析：作AF⊥BC于F，根据等腰三角形三线合一的性质得出BF=CF=4，然后根据勾股定理求得AF=3，连接AP，根据△ABC的面积=△ABP的面积+△ACP的面积解出答案即可.