题目内容
3.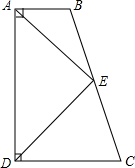 如图,在直角梯形ABCD中,AB∥CD,∠ADC=90°,∠C=70°,点E是BC的中点,CD=CE,则∠EAD的度数为( )
如图,在直角梯形ABCD中,AB∥CD,∠ADC=90°,∠C=70°,点E是BC的中点,CD=CE,则∠EAD的度数为( )| A. | 35° | B. | 45° | C. | 55° | D. | 65° |
分析 过E作EF∥AB交AD于F,于是得到AB∥EF∥CD,证得EF是梯形的中位线,于是得到AF=DF,根据平行线的性质得到∠CDE=∠DEF,∠AEF=∠BAE,∠ADC+∠DFE=180°,推出EF⊥AD,于是得到直线EF是AD的垂直平分线 根据等腰三角形的性质即可得到结论.
解答  证明:过E作EF∥AB交AD于F,
证明:过E作EF∥AB交AD于F,
∵AB∥CD,
∴AB∥EF∥CD,
∵E是BC的中点
∴EF是梯形的中位线,
∴AF=DF,
∵AB∥EF∥CD,
∴∠CDE=∠DEF,∠AEF=∠BAE,∠ADC+∠DFE=180°,
∵∠ADC=90°,
∴EF⊥AD,
∴直线EF是AD的垂直平分线
∴AE=DE,
∵CD=CE,
∴∠CDE=∠CED,
∵∠C=70°,
∴∠CDE=55°,
∴∠EDA=90°-55°=35°,
∵AE=DE,
∴∠EAD=∠EDA=35°.
故选A.
点评 本题考查了直角梯形的性质,等腰三角形的判定和性质,梯形的中位线,正确的作出辅助线是解题的关键.

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目
13.若a>0,b<0,且|a|<|b|,则a+b等于( )
| A. | -(|b|-|a|) | B. | -(|a|-|b|) | C. | -(|a|+|b|) | D. | |a|+|b| |
8.下列因式分解正确的是( )
| A. | m(a-b)+n(a-b)=(a-b)mn | B. | m(x-y)-n(y-x)=(x-y)(m-n) | ||
| C. | mn(x+y)+mn=(x+y+1)mn | D. | 3(y-x)2+2(x-y)=(x-y)(2x-3y-2) |
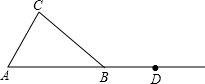 如图,在△ABC中,AB=BC,点D在AB的延长线上.
如图,在△ABC中,AB=BC,点D在AB的延长线上. 如图,DE是△ABC中AC边上的垂直平分线,如果BC=8cm,AB=14cm,则△EBC的周长为22cm.
如图,DE是△ABC中AC边上的垂直平分线,如果BC=8cm,AB=14cm,则△EBC的周长为22cm.