题目内容
12.在一个边长为(6$\sqrt{15}$+5$\sqrt{5}$)的正方形内部挖去一个边长为(6$\sqrt{15}$-5$\sqrt{5}$)的正方形,求剩余部分的面积.分析 直接利用正方形面积求法结合乘法公式计算得出答案.
解答 解:由题意可得,
剩余部分的面积为:(6$\sqrt{15}$+5$\sqrt{5}$)2-(6$\sqrt{15}$-5$\sqrt{5}$)2
=[(6$\sqrt{15}$+5$\sqrt{5}$)-(6$\sqrt{15}$-5$\sqrt{5}$)][(6$\sqrt{15}$+5$\sqrt{5}$)+(6$\sqrt{15}$-5$\sqrt{5}$)]
=10$\sqrt{5}$×12$\sqrt{15}$
=600$\sqrt{3}$.
点评 此题主要考查了二次根式的应用,正确应用乘法公式是解题关键.

练习册系列答案
 计算高手系列答案
计算高手系列答案
相关题目
17.点P(1,-2)关于x轴的对称点是P1,P1的坐标为( )
| A. | (1,-2) | B. | (-1,2) | C. | (1,2) | D. | (-2,-1) |
4.已知抛物线y=ax2与双曲线y=-$\frac{2}{x}$交点的横坐标大于0,则a的取值范围是( )
| A. | a>0 | B. | a<0 | C. | a>-2 | D. | a<-2 |
19.解方程组:①$\left\{\begin{array}{l}{y=2x-1}\\{7x+5y=8}\end{array}\right.$,②$\left\{\begin{array}{l}{8x+6y=25}\\{17x-6y=48}\end{array}\right.$,在下列提供的两题解法中,较为简便的是( )
| A. | ①②均用代入法 | B. | ①②均用加减法 | ||
| C. | ①用代入法,②用加减法 | D. | ①用加减法,②用代入法 |

 +1 B. -
+1 B. -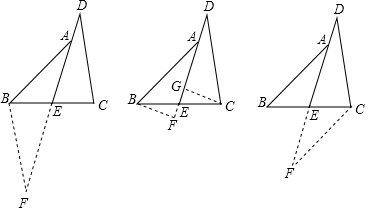
 数a,b在数轴上对应点A,B的位置如图所示,且|a|=2,b是16的一个平方根,求式子|a+b|-$\sqrt{{a}^{2}}$-$\root{3}{(a-b)^{3}}$的值.
数a,b在数轴上对应点A,B的位置如图所示,且|a|=2,b是16的一个平方根,求式子|a+b|-$\sqrt{{a}^{2}}$-$\root{3}{(a-b)^{3}}$的值.